학습 참고 문서
공식 Sample Project 링크
https://github.com/Unity-Technologies/EntityComponentSystemSamples/tree/master
멀티코어 CPU를 활용하기 위해 Job을 사용하는 기본적인 방법
STEP
– 싱글 스레드 잡을 생성, 예약, 완료
– 병렬 잡을 생성, 예약, 완료
– 다른 잡에 종속되는 잡을 예약
– NativeArrays를 사용
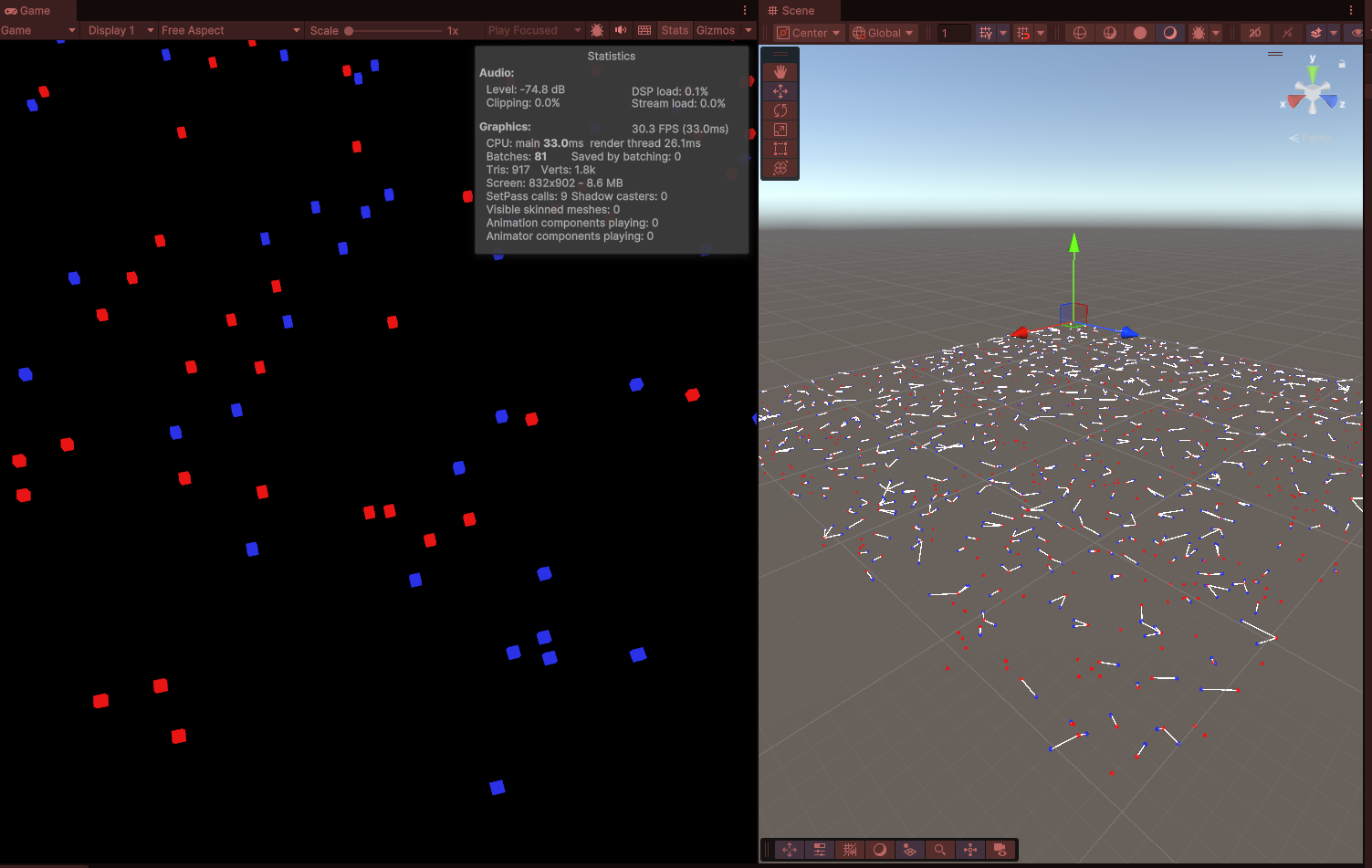
파란 큐브와 빨간 큐브를 각각 Seeker와 Target으로 정하고 각Seeker은 가장 가까운 Target으로 이어지는 디버그 라인을 추가합니다.
각 Step은 서로 다른 방식으로 문제를 해결하여 Step마다 성능 비교를 할 수 있습니다.
SeekerPrefab의 인스턴스를 생성 -> 2D 평면을 따라 무작위 방향과 무작위 위치를 설정 ->
Target도 동일한 방식으로 생성 -> 모든 Seeker와 Target의 트랜스폼을 정적 배열에 할당하여
FindNearest 스크립트에서 액세스하여 Update()
Step 1. Scene – No Job
일반적인 브루트 포스 순회 방법, 각 Seeker 마다 모든 Target과의 거리를 확인
Spawner.cs
using UnityEngine;
namespace Tutorials.Jobs.Step1
{
public class Spawner : MonoBehaviour
{
// The set of targets is fixed, so rather than
// retrieve the targets every frame, we'll cache
// their transforms in this field.
public static Transform[] TargetTransforms;
public GameObject SeekerPrefab;
public GameObject TargetPrefab;
public int NumSeekers;
public int NumTargets;
public Vector2 Bounds;
public void Start()
{
Random.InitState(123);
for (int i = 0; i < NumSeekers; i++)
{
GameObject go = GameObject.Instantiate(SeekerPrefab);
Seeker seeker = go.GetComponent<Seeker>();
Vector2 dir = Random.insideUnitCircle;
seeker.Direction = new Vector3(dir.x, 0, dir.y);
go.transform.localPosition = new Vector3(
Random.Range(0, Bounds.x), 0, Random.Range(0, Bounds.y));
}
TargetTransforms = new Transform[NumTargets];
for (int i = 0; i < NumTargets; i++)
{
GameObject go = GameObject.Instantiate(TargetPrefab);
Target target = go.GetComponent<Target>();
Vector2 dir = Random.insideUnitCircle;
target.Direction = new Vector3(dir.x, 0, dir.y);
TargetTransforms[i] = go.transform;
go.transform.localPosition = new Vector3(
Random.Range(0, Bounds.x), 0, Random.Range(0, Bounds.y));
}
}
}
}
Seeker.cs
using UnityEngine;
namespace Tutorials.Jobs.Step1
{
public class Seeker : MonoBehaviour
{
public Vector3 Direction;
public void Update()
{
transform.localPosition += Direction * Time.deltaTime;
}
}
}
Target.cs
using UnityEngine;
namespace Tutorials.Jobs.Step1
{
public class Target : MonoBehaviour
{
public Vector3 Direction;
public void Update()
{
transform.localPosition += Direction * Time.deltaTime;
}
}
}
FindNearest.cs
using UnityEngine;
namespace Tutorials.Jobs.Step1
{
public class FindNearest : MonoBehaviour
{
public void Update()
{
// Find nearest Target.
// When comparing distances, it's cheaper to compare
// the squares of the distances because doing so
// avoids computing square roots.
Vector3 nearestTargetPosition = default;
float nearestDistSq = float.MaxValue;
foreach (var targetTransform in Spawner.TargetTransforms)
{
Vector3 offset = targetTransform.localPosition - transform.localPosition;
float distSq = offset.sqrMagnitude;
if (distSq < nearestDistSq)
{
nearestDistSq = distSq;
nearestTargetPosition = targetTransform.localPosition;
}
}
Debug.DrawLine(transform.localPosition, nearestTargetPosition);
}
}
}
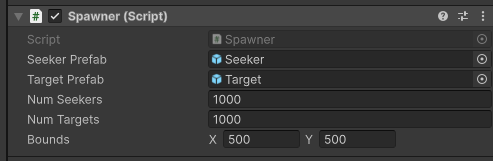
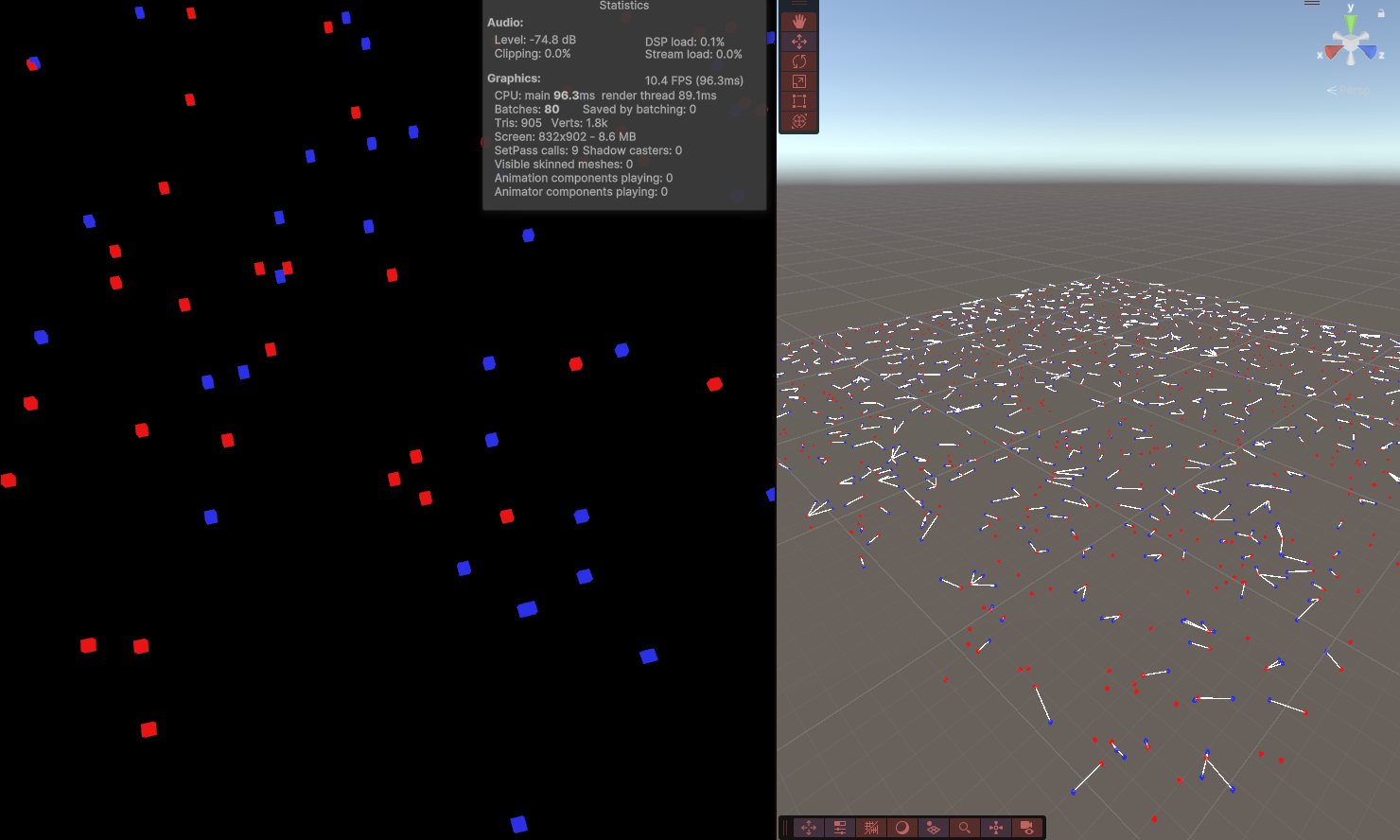
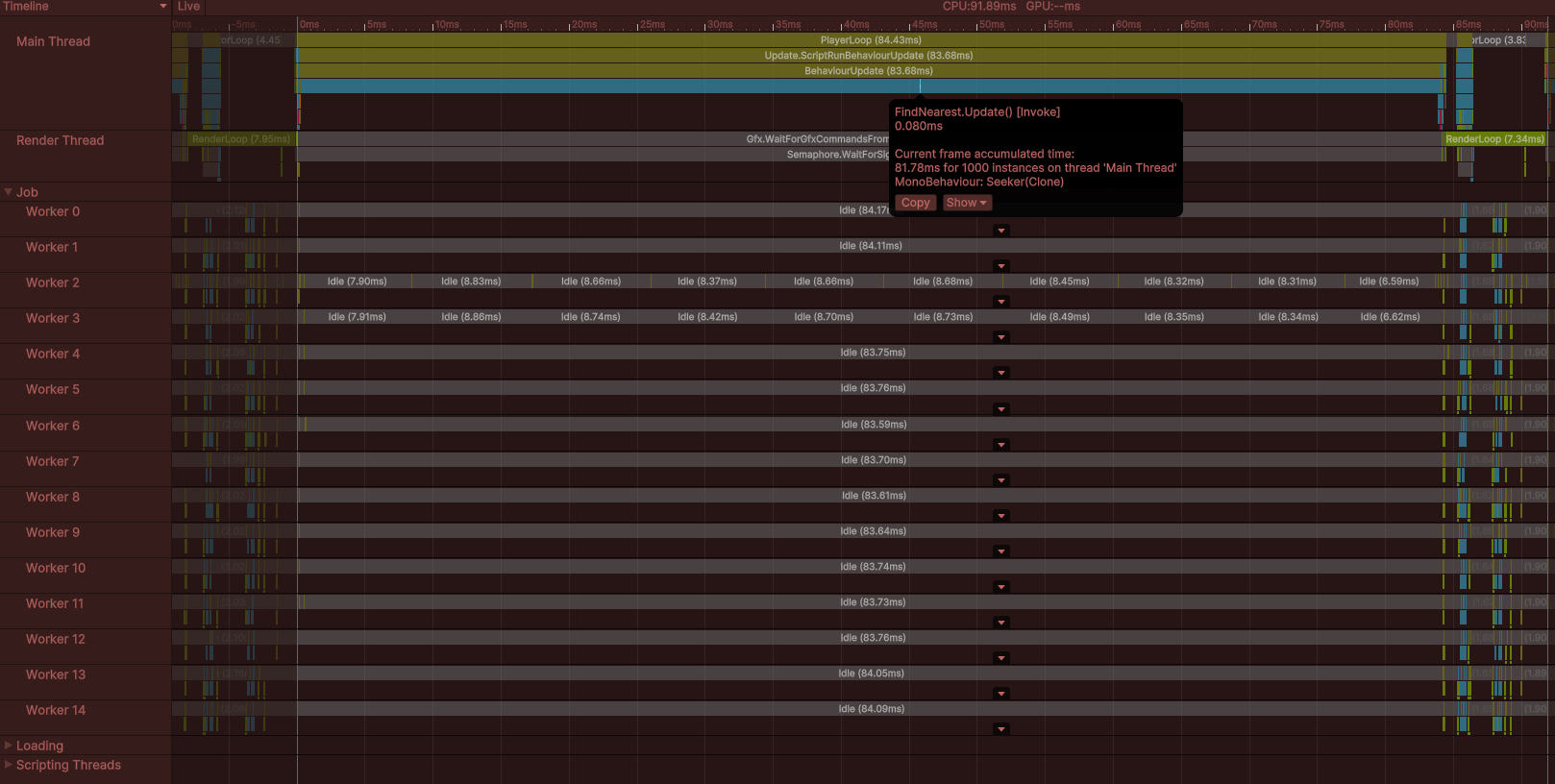
Seeker의 1000개의 FindNearest가 Update()를 수행하면서 약 82ms를 프레임마다 실행 (개당 0.082ms)
Step 2. Scene – SingleThreadedJob
일반적인 브루트 포스 순회 방법, 하나의 FindNearest에서 Target과의 거리를 확인
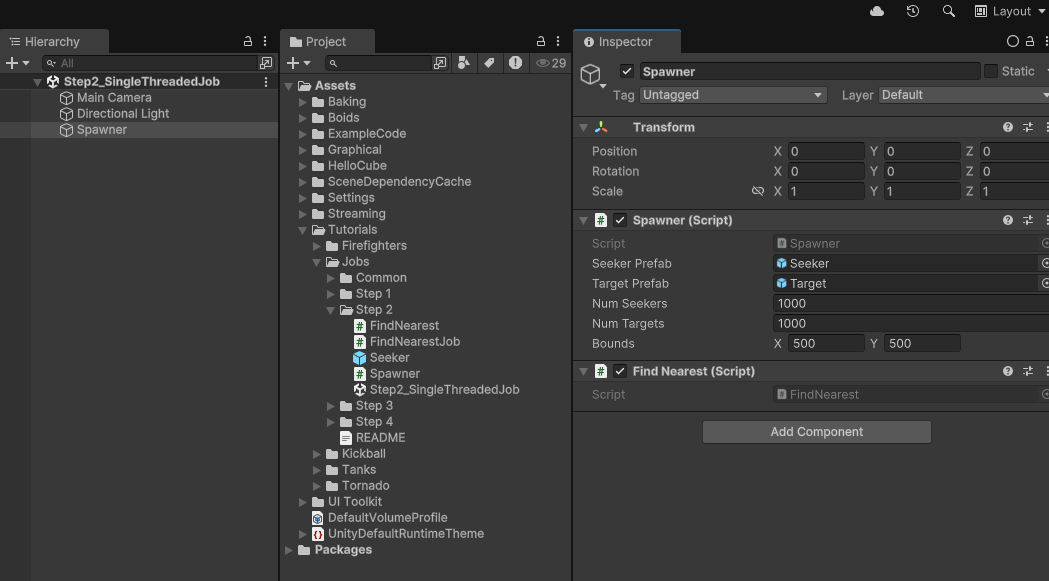
Spawner.cs
using UnityEngine;
using Seeker = Tutorials.Jobs.Step1.Seeker;
using Target = Tutorials.Jobs.Step1.Target;
namespace Tutorials.Jobs.Step2
{
public class Spawner : MonoBehaviour
{
public static Transform[] TargetTransforms;
// Cache the seeker transforms.
public static Transform[] SeekerTransforms;
public GameObject SeekerPrefab;
public GameObject TargetPrefab;
public int NumSeekers;
public int NumTargets;
public Vector2 Bounds;
public void Start()
{
Random.InitState(123);
SeekerTransforms = new Transform[NumSeekers];
for (int i = 0; i < NumSeekers; i++)
{
GameObject go = GameObject.Instantiate(SeekerPrefab);
Seeker seeker = go.GetComponent<Seeker>();
Vector2 dir = Random.insideUnitCircle;
seeker.Direction = new Vector3(dir.x, 0, dir.y);
SeekerTransforms[i] = go.transform;
go.transform.localPosition = new Vector3(
Random.Range(0, Bounds.x), 0, Random.Range(0, Bounds.y));
}
TargetTransforms = new Transform[NumTargets];
for (int i = 0; i < NumTargets; i++)
{
GameObject go = GameObject.Instantiate(TargetPrefab);
Target target = go.GetComponent<Target>();
Vector2 dir = Random.insideUnitCircle;
target.Direction = new Vector3(dir.x, 0, dir.y);
TargetTransforms[i] = go.transform;
go.transform.localPosition = new Vector3(
Random.Range(0, Bounds.x), 0, Random.Range(0, Bounds.y));
}
}
}
}
FindNearest.cs
using Unity.Collections;
using Unity.Jobs;
using Unity.Mathematics;
using UnityEngine;
namespace Tutorials.Jobs.Step2
{
public class FindNearest : MonoBehaviour
{
// The size of our arrays does not need to vary, so rather than create
// new arrays every field, we'll create the arrays in Awake() and store them
// in these fields.
NativeArray<float3> TargetPositions;
NativeArray<float3> SeekerPositions;
NativeArray<float3> NearestTargetPositions;
public void Start()
{
Spawner spawner = Object.FindFirstObjectByType<Spawner>();
// We use the Persistent allocator because these arrays must
// exist for the run of the program.
TargetPositions = new NativeArray<float3>(spawner.NumTargets, Allocator.Persistent);
SeekerPositions = new NativeArray<float3>(spawner.NumSeekers, Allocator.Persistent);
NearestTargetPositions = new NativeArray<float3>(spawner.NumSeekers, Allocator.Persistent);
}
// We are responsible for disposing of our allocations
// when we no longer need them.
public void OnDestroy()
{
TargetPositions.Dispose();
SeekerPositions.Dispose();
NearestTargetPositions.Dispose();
}
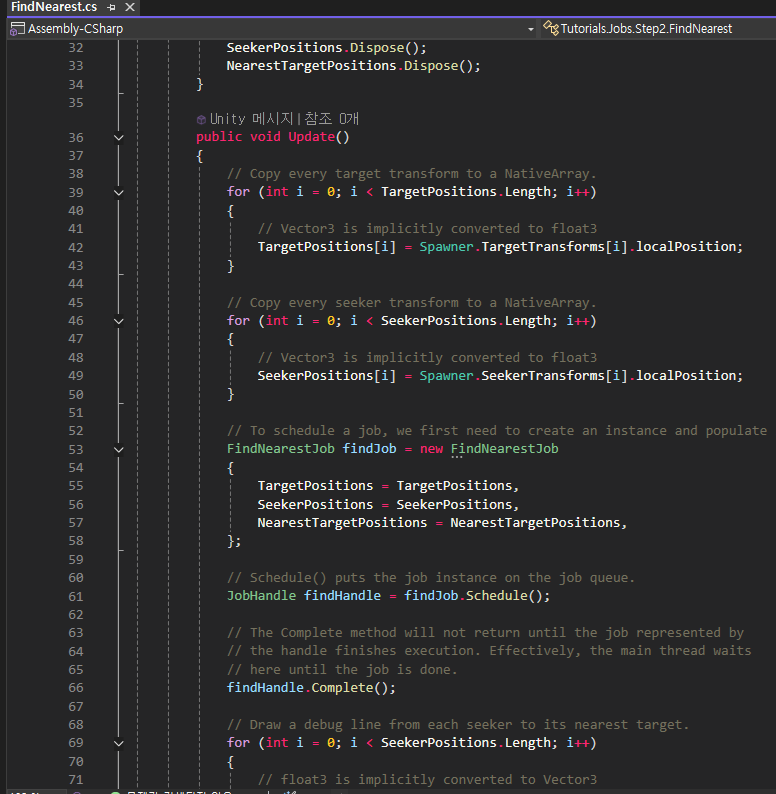
public void Update()
{
// Copy every target transform to a NativeArray.
for (int i = 0; i < TargetPositions.Length; i++)
{
// Vector3 is implicitly converted to float3
TargetPositions[i] = Spawner.TargetTransforms[i].localPosition;
}
// Copy every seeker transform to a NativeArray.
for (int i = 0; i < SeekerPositions.Length; i++)
{
// Vector3 is implicitly converted to float3
SeekerPositions[i] = Spawner.SeekerTransforms[i].localPosition;
}
// To schedule a job, we first need to create an instance and populate its fields.
FindNearestJob findJob = new FindNearestJob
{
TargetPositions = TargetPositions,
SeekerPositions = SeekerPositions,
NearestTargetPositions = NearestTargetPositions,
};
// Schedule() puts the job instance on the job queue.
JobHandle findHandle = findJob.Schedule();
// The Complete method will not return until the job represented by
// the handle finishes execution. Effectively, the main thread waits
// here until the job is done.
findHandle.Complete();
// Draw a debug line from each seeker to its nearest target.
for (int i = 0; i < SeekerPositions.Length; i++)
{
// float3 is implicitly converted to Vector3
Debug.DrawLine(SeekerPositions[i], NearestTargetPositions[i]);
}
}
}
}
FindNearestJob.cs
using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;
// We'll use Unity.Mathematics.float3 instead of Vector3,
// and we'll use Unity.Mathematics.math.distancesq instead of Vector3.sqrMagnitude.
using Unity.Mathematics;
namespace Tutorials.Jobs.Step2
{
// Include the BurstCompile attribute to Burst compile the job.
[BurstCompile]
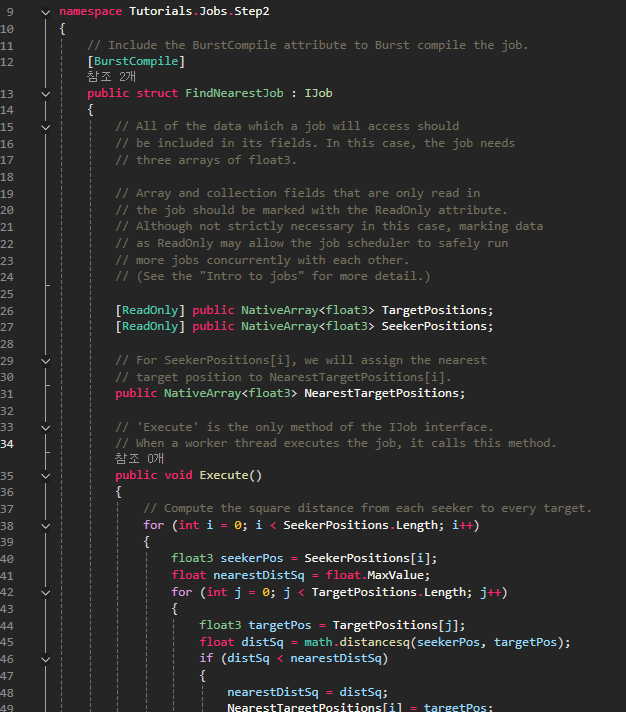
public struct FindNearestJob : IJob
{
// All of the data which a job will access should
// be included in its fields. In this case, the job needs
// three arrays of float3.
// Array and collection fields that are only read in
// the job should be marked with the ReadOnly attribute.
// Although not strictly necessary in this case, marking data
// as ReadOnly may allow the job scheduler to safely run
// more jobs concurrently with each other.
// (See the "Intro to jobs" for more detail.)
[ReadOnly] public NativeArray<float3> TargetPositions;
[ReadOnly] public NativeArray<float3> SeekerPositions;
// For SeekerPositions[i], we will assign the nearest
// target position to NearestTargetPositions[i].
public NativeArray<float3> NearestTargetPositions;
// 'Execute' is the only method of the IJob interface.
// When a worker thread executes the job, it calls this method.
public void Execute()
{
// Compute the square distance from each seeker to every target.
for (int i = 0; i < SeekerPositions.Length; i++)
{
float3 seekerPos = SeekerPositions[i];
float nearestDistSq = float.MaxValue;
for (int j = 0; j < TargetPositions.Length; j++)
{
float3 targetPos = TargetPositions[j];
float distSq = math.distancesq(seekerPos, targetPos);
if (distSq < nearestDistSq)
{
nearestDistSq = distSq;
NearestTargetPositions[i] = targetPos;
}
}
}
}
}
}
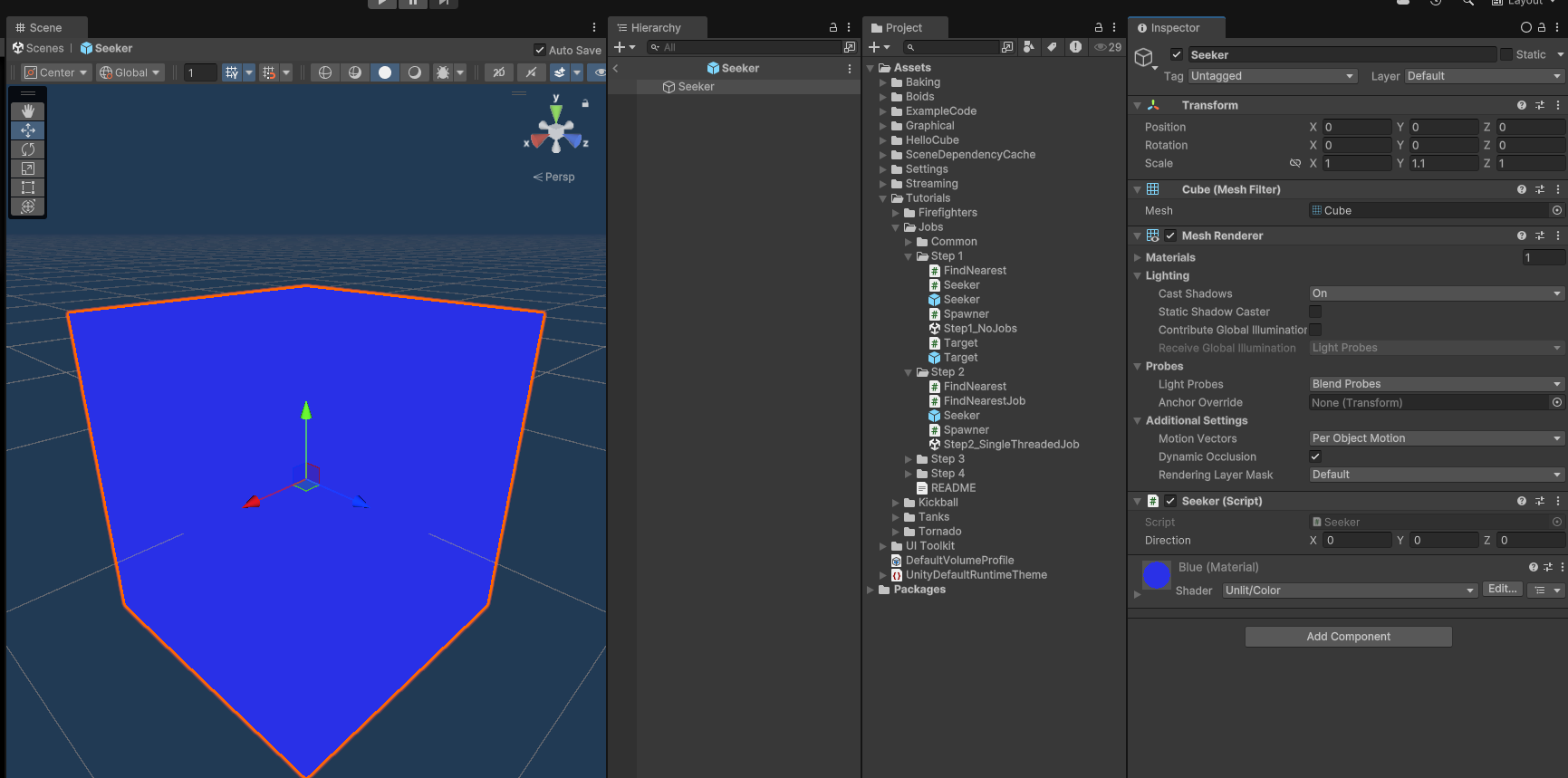
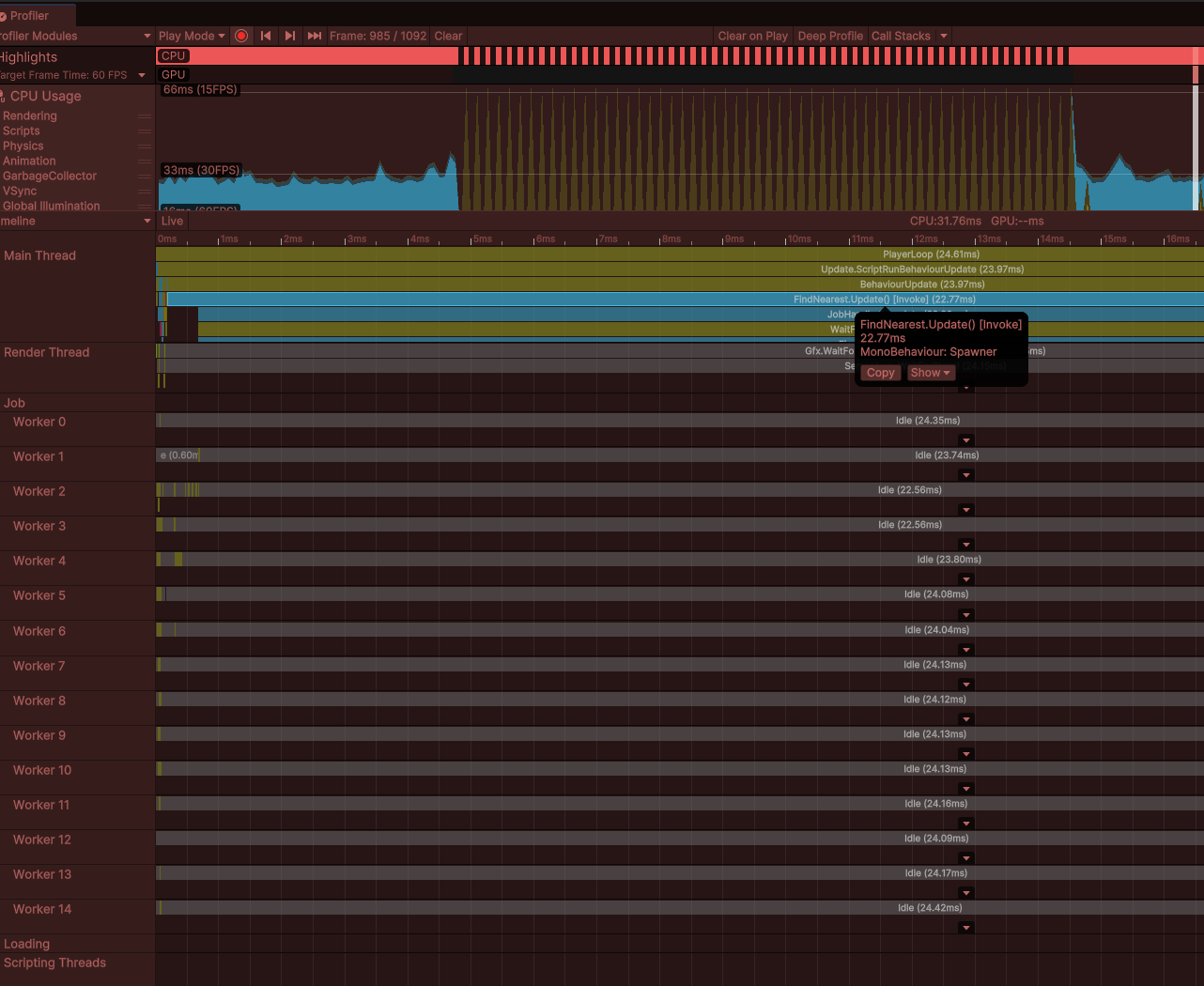
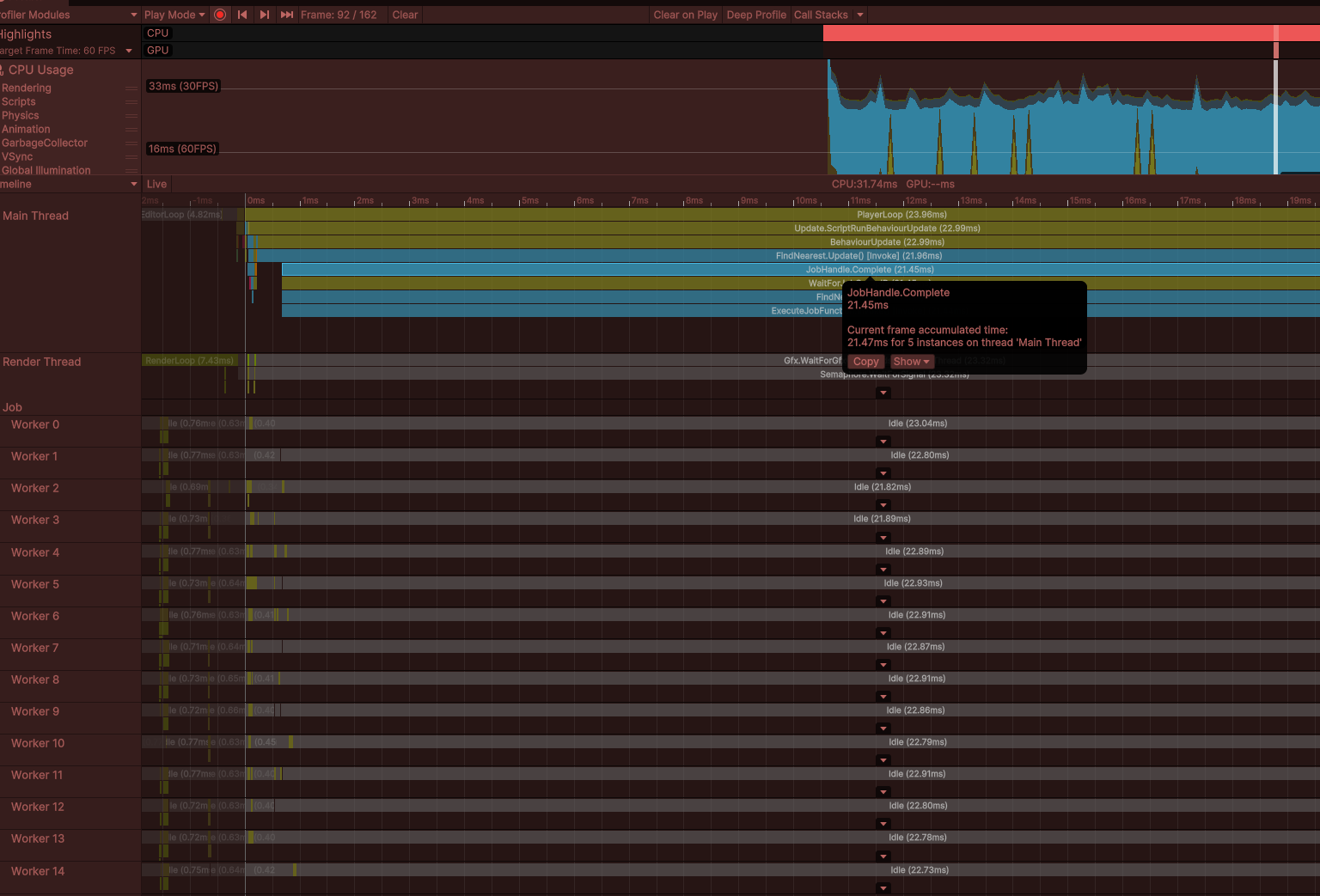
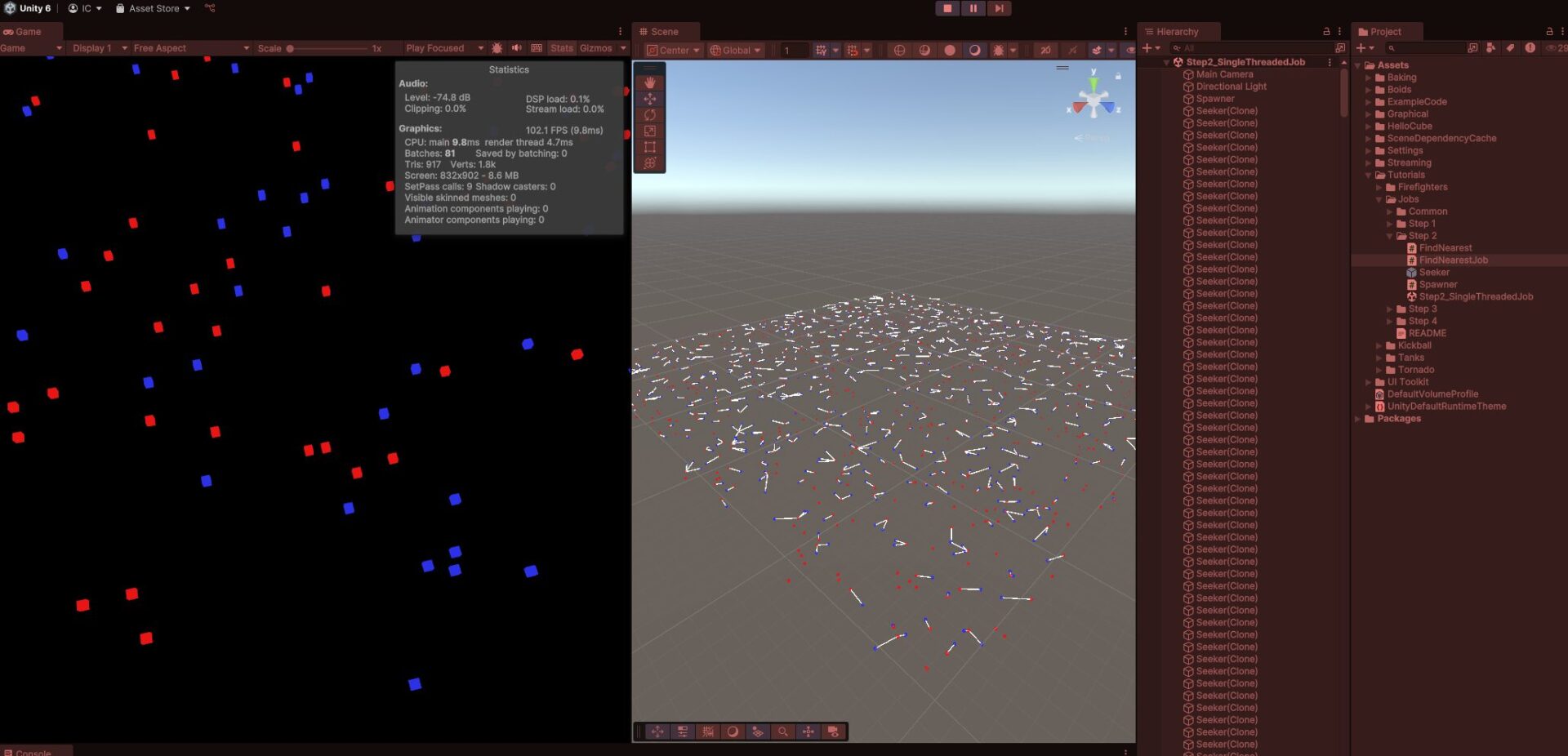
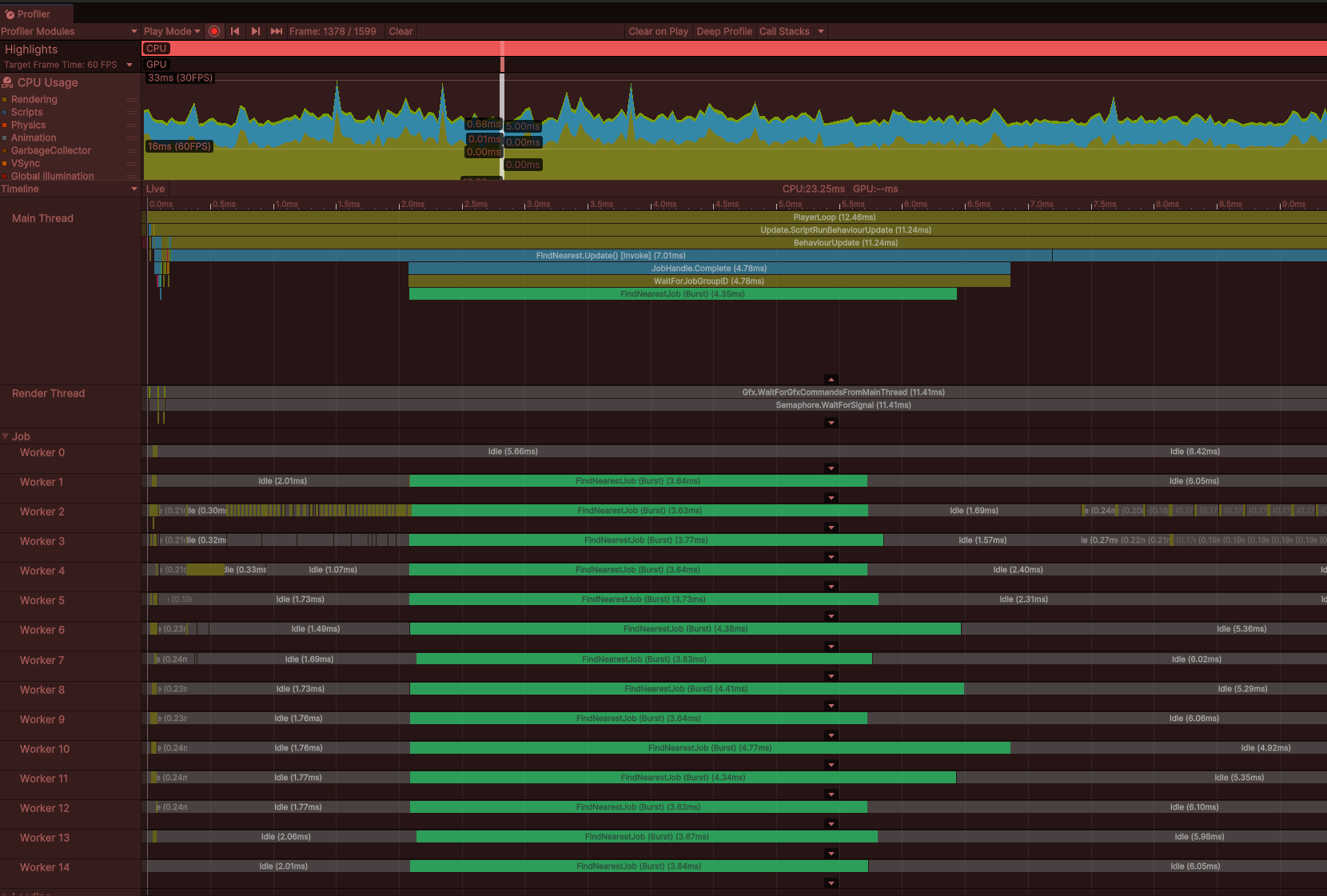
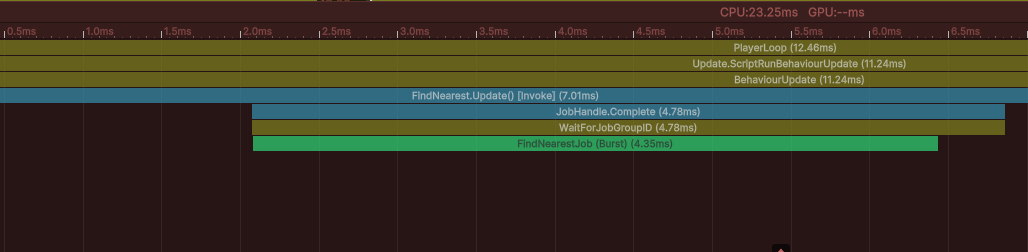
FindNearest 업데이트 자체는 아무것도 하지 않고 잡이 실행 및 완료될 것을 기다리고 있음
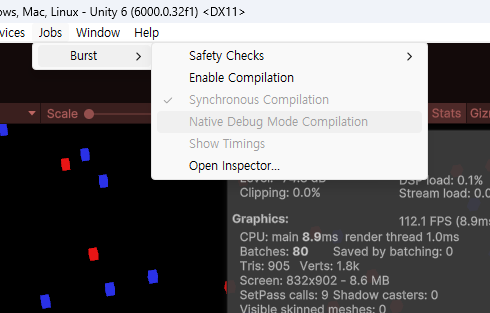
Step 1 보다 성능이 향상된 원인은 Step 1의 Seeker의 Update() 1000개에 대한 오버헤드가 발생되지 않음 (오직 1개)
트랜스폼을 순회할 때 메모리를 건너 뛰면서 트랜스폼에 액세스했는데 이는 캐시에 부하주는 작업을 배열로 변경하여 성능을 향상시킴
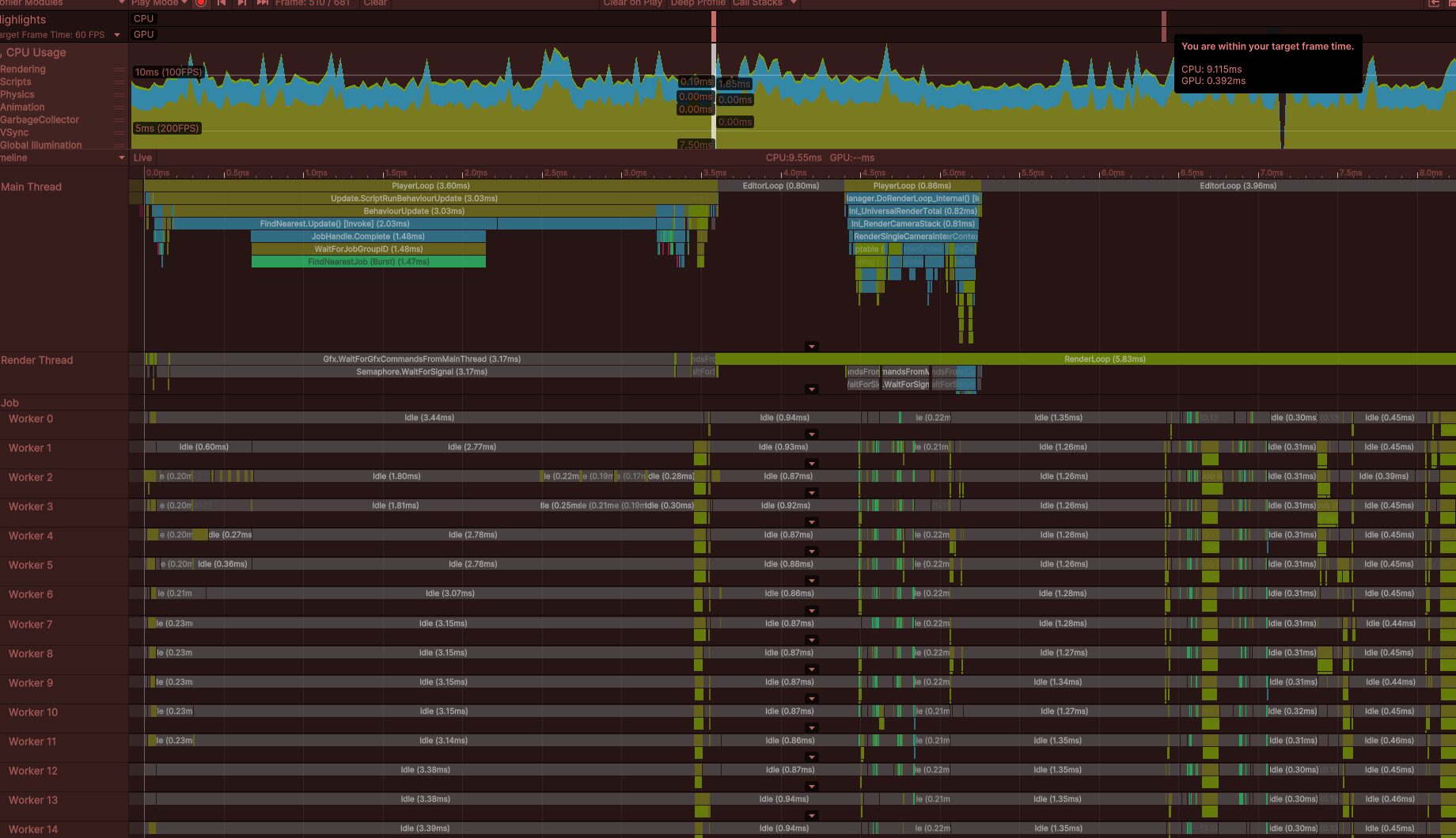
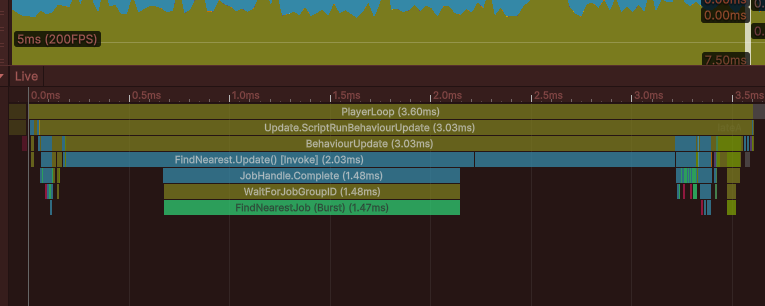
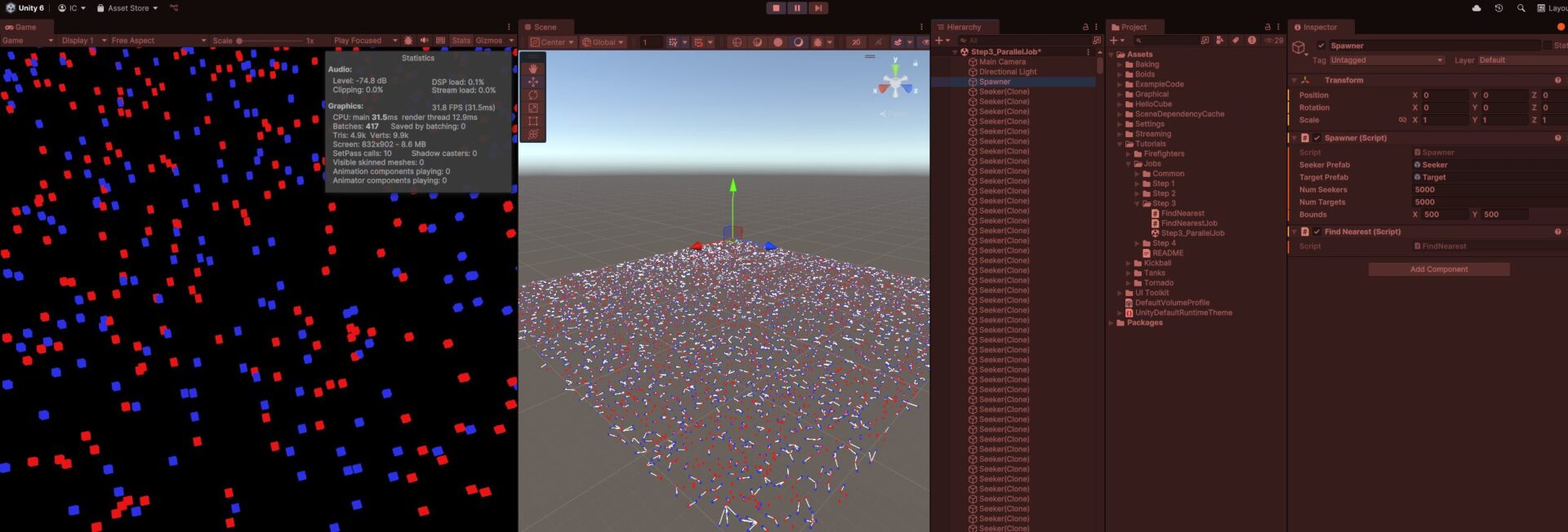
Step 3. Scene – ParallelJob
일반적인 브루트 포스 순회 방법, 하나의 FindNearest에서 Target과의 거리를 확인
FindNearest.cs
using Spawner = Tutorials.Jobs.Step2.Spawner;
using Unity.Collections;
using Unity.Jobs;
using Unity.Mathematics;
using UnityEngine;
namespace Tutorials.Jobs.Step3
{
// Exactly the same as in prior step except this schedules a parallel job instead of a single-threaded job.
public class FindNearest : MonoBehaviour
{
NativeArray<float3> TargetPositions;
NativeArray<float3> SeekerPositions;
NativeArray<float3> NearestTargetPositions;
public void Start()
{
Spawner spawner = GetComponent<Spawner>();
TargetPositions = new NativeArray<float3>(spawner.NumTargets, Allocator.Persistent);
SeekerPositions = new NativeArray<float3>(spawner.NumSeekers, Allocator.Persistent);
NearestTargetPositions = new NativeArray<float3>(spawner.NumSeekers, Allocator.Persistent);
}
public void OnDestroy()
{
TargetPositions.Dispose();
SeekerPositions.Dispose();
NearestTargetPositions.Dispose();
}
public void Update()
{
for (int i = 0; i < TargetPositions.Length; i++)
{
TargetPositions[i] = Spawner.TargetTransforms[i].localPosition;
}
for (int i = 0; i < SeekerPositions.Length; i++)
{
SeekerPositions[i] = Spawner.SeekerTransforms[i].localPosition;
}
FindNearestJob findJob = new FindNearestJob
{
TargetPositions = TargetPositions,
SeekerPositions = SeekerPositions,
NearestTargetPositions = NearestTargetPositions,
};
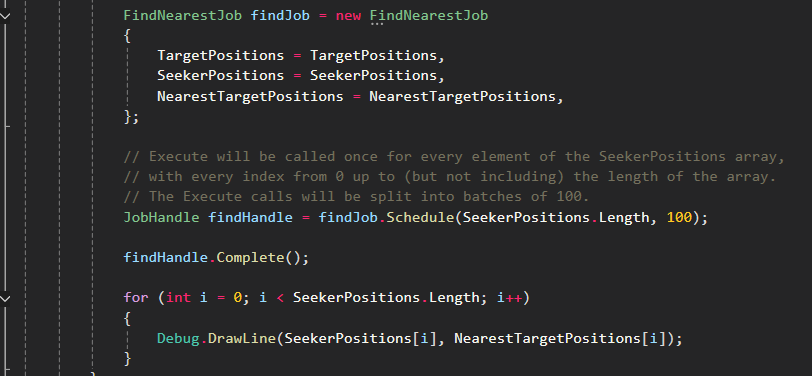
// Execute will be called once for every element of the SeekerPositions array,
// with every index from 0 up to (but not including) the length of the array.
// The Execute calls will be split into batches of 100.
JobHandle findHandle = findJob.Schedule(SeekerPositions.Length, 100);
findHandle.Complete();
for (int i = 0; i < SeekerPositions.Length; i++)
{
Debug.DrawLine(SeekerPositions[i], NearestTargetPositions[i]);
}
}
}
}
FindNearestJob.cs
using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;
using Unity.Mathematics;
namespace Tutorials.Jobs.Step3
{
[BurstCompile]
public struct FindNearestJob : IJobParallelFor
{
[ReadOnly] public NativeArray<float3> TargetPositions;
[ReadOnly] public NativeArray<float3> SeekerPositions;
public NativeArray<float3> NearestTargetPositions;
public void Execute(int index)
{
float3 seekerPos = SeekerPositions[index];
float nearestDistSq = float.MaxValue;
for (int i = 0; i < TargetPositions.Length; i++)
{
float3 targetPos = TargetPositions[i];
float distSq = math.distancesq(seekerPos, targetPos);
if (distSq < nearestDistSq)
{
nearestDistSq = distSq;
NearestTargetPositions[index] = targetPos;
}
}
}
}
}
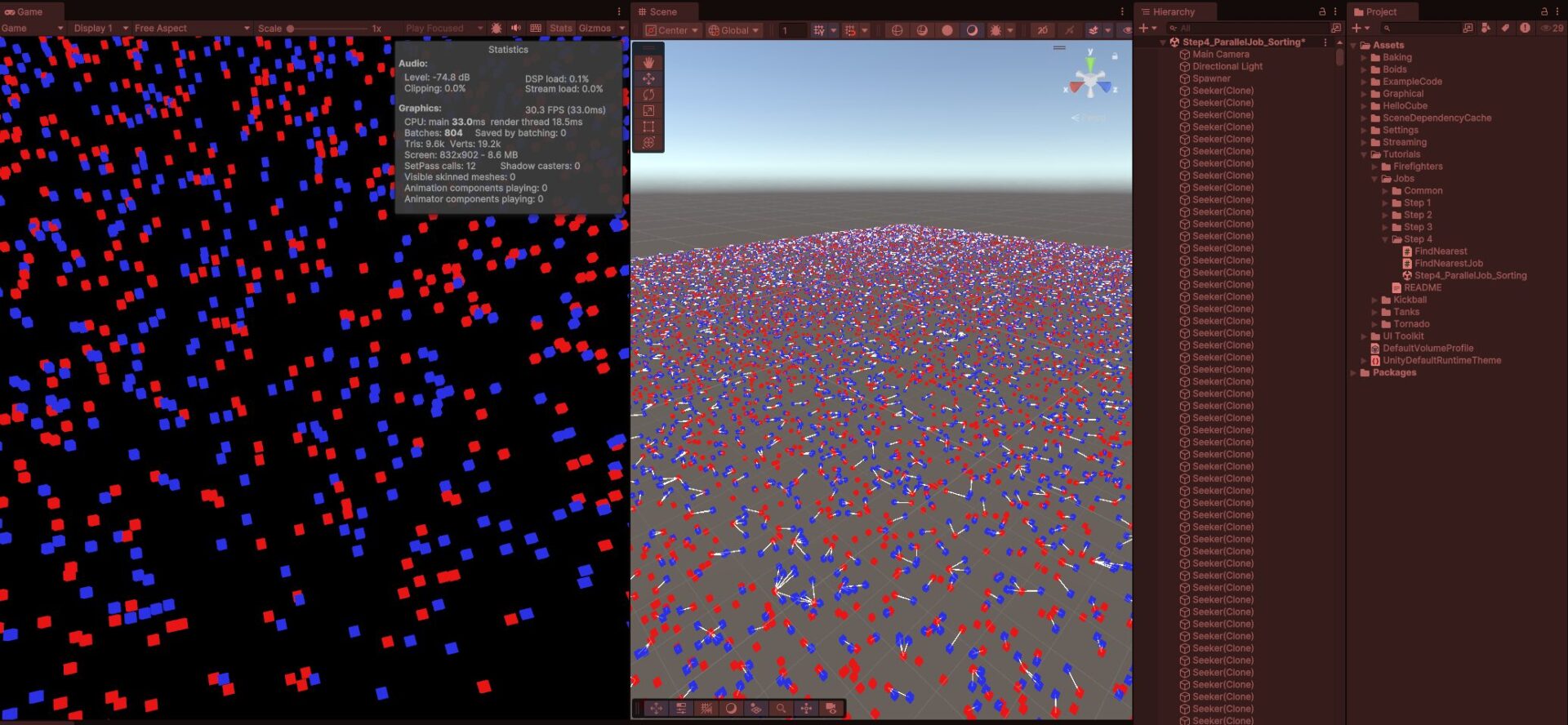
Step 4. Scene – ParallelJob_Sorting
정렬을 이용한 병렬 작업
FindNearest.cs
using Unity.Collections;
using Unity.Jobs;
using Unity.Mathematics;
using UnityEngine;
using Spawner = Tutorials.Jobs.Step2.Spawner;
namespace Tutorials.Jobs.Step4
{
public class FindNearest : MonoBehaviour
{
NativeArray<float3> TargetPositions;
NativeArray<float3> SeekerPositions;
NativeArray<float3> NearestTargetPositions;
public void Start()
{
Spawner spawner = GetComponent<Spawner>();
TargetPositions = new NativeArray<float3>(spawner.NumTargets, Allocator.Persistent);
SeekerPositions = new NativeArray<float3>(spawner.NumSeekers, Allocator.Persistent);
NearestTargetPositions = new NativeArray<float3>(spawner.NumSeekers, Allocator.Persistent);
}
public void OnDestroy()
{
TargetPositions.Dispose();
SeekerPositions.Dispose();
NearestTargetPositions.Dispose();
}
public void Update()
{
for (int i = 0; i < TargetPositions.Length; i++)
{
TargetPositions[i] = Spawner.TargetTransforms[i].localPosition;
}
for (int i = 0; i < SeekerPositions.Length; i++)
{
SeekerPositions[i] = Spawner.SeekerTransforms[i].localPosition;
}
SortJob<float3, AxisXComparer> sortJob = TargetPositions.SortJob(new AxisXComparer { });
FindNearestJob findJob = new FindNearestJob
{
TargetPositions = TargetPositions,
SeekerPositions = SeekerPositions,
NearestTargetPositions = NearestTargetPositions,
};
JobHandle sortHandle = sortJob.Schedule();
JobHandle findHandle = findJob.Schedule(SeekerPositions.Length, 100, sortHandle);
findHandle.Complete();
for (int i = 0; i < SeekerPositions.Length; i++)
{
Debug.DrawLine(SeekerPositions[i], NearestTargetPositions[i]);
}
}
}
}
FindNearestJob.cs
using System.Collections.Generic;
using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;
using Unity.Mathematics;
namespace Tutorials.Jobs.Step4
{
[BurstCompile]
public struct FindNearestJob : IJobParallelFor
{
[ReadOnly] public NativeArray<float3> TargetPositions;
[ReadOnly] public NativeArray<float3> SeekerPositions;
public NativeArray<float3> NearestTargetPositions;
public void Execute(int index)
{
float3 seekerPos = SeekerPositions[index];
// Find the target with the closest X coord.
int startIdx = TargetPositions.BinarySearch(seekerPos, new AxisXComparer { });
// When no precise match is found, BinarySearch returns the bitwise negation of the last-searched offset.
// So when startIdx is negative, we flip the bits again, but we then must ensure the index is within bounds.
if (startIdx < 0) startIdx = ~startIdx;
if (startIdx >= TargetPositions.Length) startIdx = TargetPositions.Length - 1;
// The position of the target with the closest X coord.
float3 nearestTargetPos = TargetPositions[startIdx];
float nearestDistSq = math.distancesq(seekerPos, nearestTargetPos);
// Searching upwards through the array for a closer target.
Search(seekerPos, startIdx + 1, TargetPositions.Length, +1, ref nearestTargetPos, ref nearestDistSq);
// Search downwards through the array for a closer target.
Search(seekerPos, startIdx - 1, -1, -1, ref nearestTargetPos, ref nearestDistSq);
NearestTargetPositions[index] = nearestTargetPos;
}
void Search(float3 seekerPos, int startIdx, int endIdx, int step,
ref float3 nearestTargetPos, ref float nearestDistSq)
{
for (int i = startIdx; i != endIdx; i += step)
{
float3 targetPos = TargetPositions[i];
float xdiff = seekerPos.x - targetPos.x;
// If the square of the x distance is greater than the current nearest, we can stop searching.
if ((xdiff * xdiff) > nearestDistSq) break;
float distSq = math.distancesq(targetPos, seekerPos);
if (distSq < nearestDistSq)
{
nearestDistSq = distSq;
nearestTargetPos = targetPos;
}
}
}
}
public struct AxisXComparer : IComparer<float3>
{
public int Compare(float3 a, float3 b)
{
return a.x.CompareTo(b.x);
}
}
}
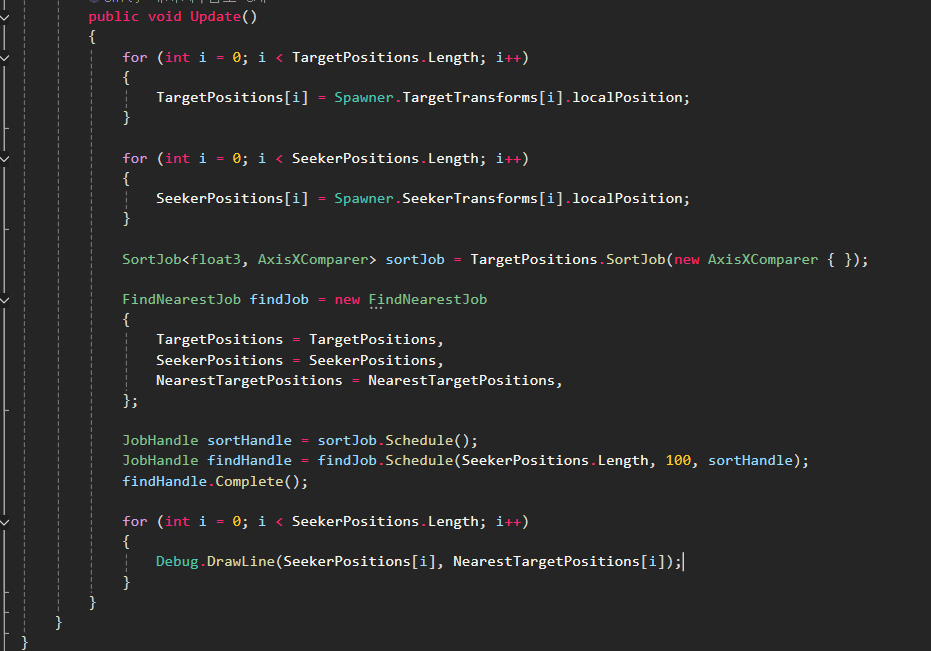
x축을 따라 TargetPositions를 정렬합니다
이어서 FindNearestJob에서 바이너리 검색을 통해 탐색기의 x 좌표와 가장 가까운 타겟의 위치를 찾고
그 인덱스 주위를 탐색해 가장 가까운 타겟을 찾습니다.
그러면 대부분의 경우 탐색기를 모든 타겟과 비교하는 대신 몇몇 타겟과만 비교하는 작업이 되어 더 간단합니다.

먼저 SortJob은 Collections 패키지의 네이티브 배열 확장 메서드로서 SortJob 구조체를 반환합니다.
그 구조체 자체는 잡이 아니지만 Schedule 메서드를 호출할 경우 하나가 아닌 두 개의 잡이 예약됩니다.
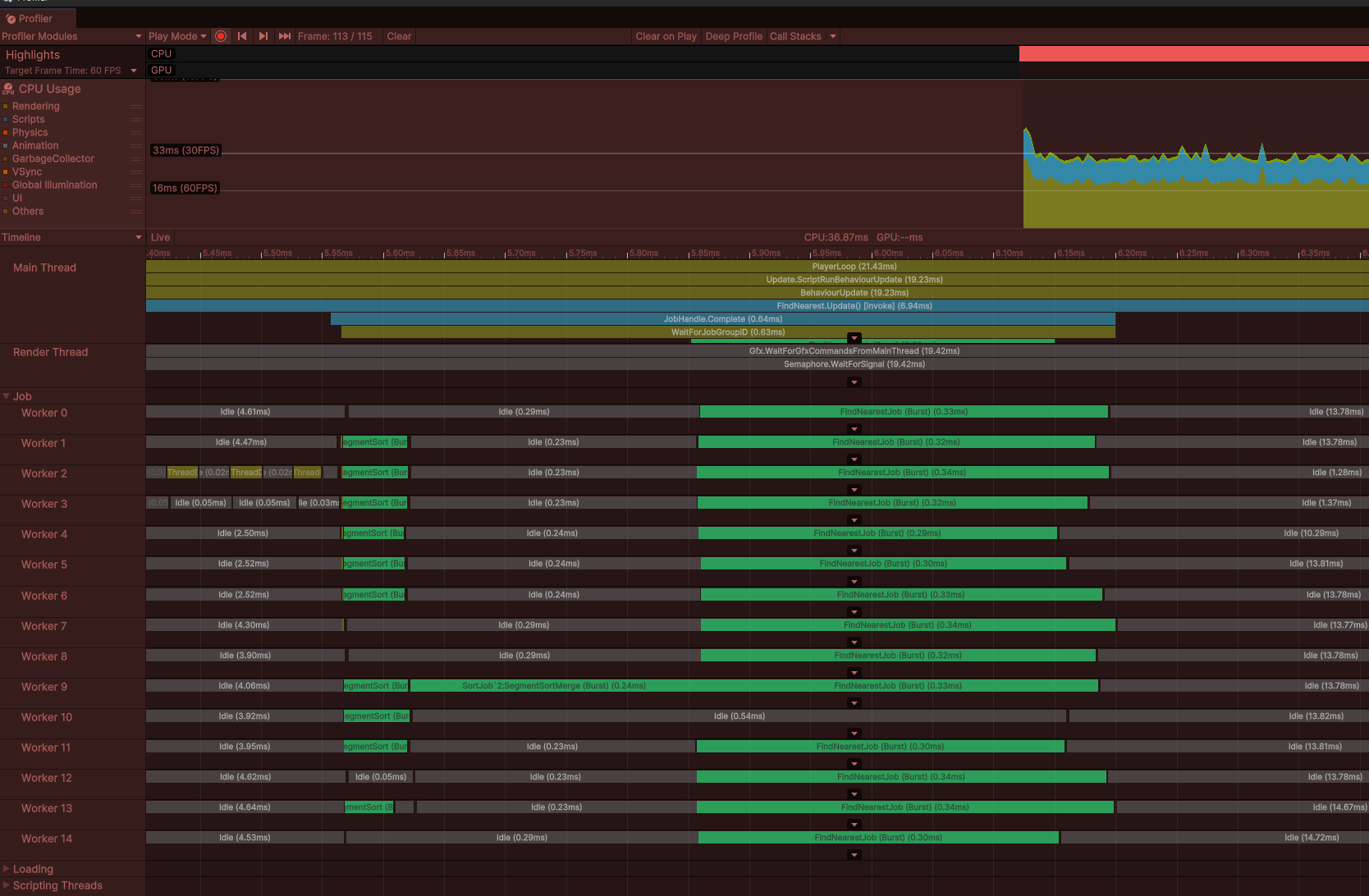
이 메서드는 먼저 segmentSortJob을 생성하고 예약하는데 이는 배열의 서로 다른 세그먼트를 독립적으로 정렬하는 병렬 잡입니다.
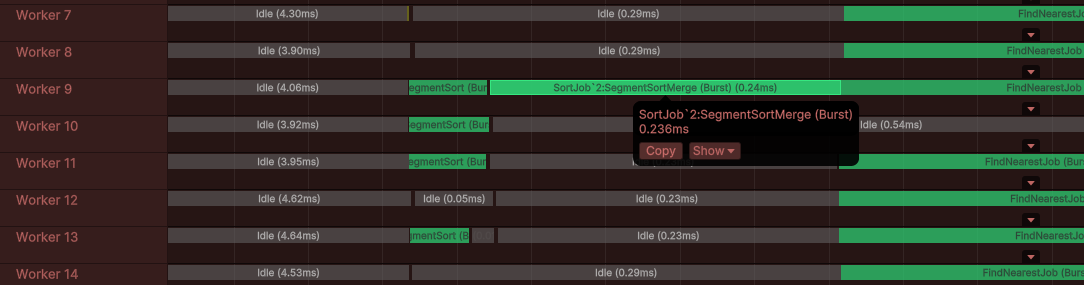
이후 두 번째 작업이자 싱글 스레드 작업이며 같은 배열 내 세그먼트들을 병합하는 SegmentSortMerge가 예약됩니다
이 두 잡은 기존 배열 내에서 MergeSort를 수행합니다.
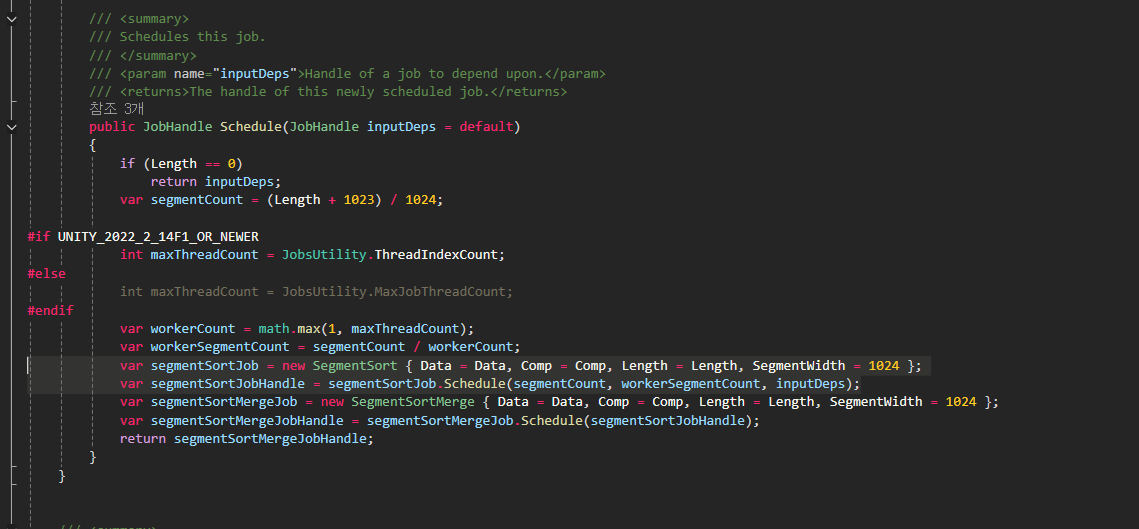
결정적으로 두 번째의 병합 잡은 세그먼트 정렬이 완료될 때까지 기다려야 합니다.
그래서 두 번째 잡을 예약할 때 첫 번째 잡의 잡 핸들을 전달하면 첫 번째 잡은 두 번째 잡의 종속 관계가 됩니다.
잡이 종속 관계를 가질 경우 워커 스레드들은 그 종속 관계의 실행이 모두 완료될 때까지 해당 잡을 실행하지 않습니다.
둘 이상의 잡을 예약해야 하며 해당 잡들의 실행 순서를 지정해야 할 때는 종속 관계를 통해 그 순서를 정할 수 있습니다.
이 코드에서 FindNearestJob을 예약할 때 sortJob 핸들을 종속성으로 전달하는데 이는 MergeSort가 완료될 때까지
이 잡의 실행이 시작되어서는 안 되기 때문입니다.
이후 잡이 완료되면 잡의 모든 종속성도 묵시적으로 완료되므로 SegmentSort, SegmentMerge, FindNearestJob의 세 잡이 모두 완료됩니다.

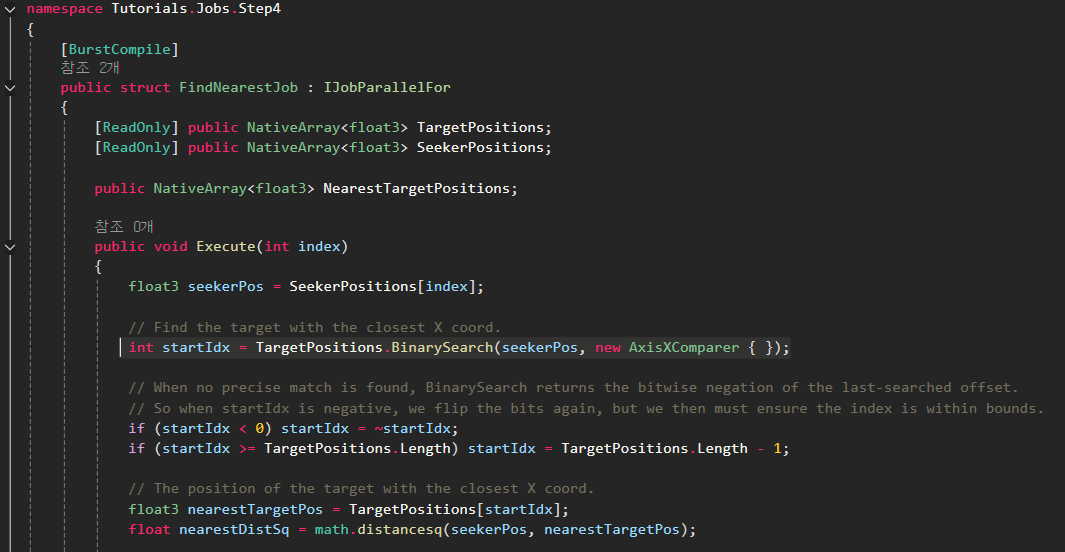
FindNearestJob을 보면 Collections 패키지의 네이티브 배열 확장 메서드인 BinarySearch를 호출하고 있습니다.
이는 단지 X 좌표와 비교해서 SeekerPos와 일치하는 TargetPositions 내 인덱스를 반환합니다.
대부분은 정확히 일치하는 결과를 찾을 수 없을 것이므로 반환되는 인덱스 값은 대부분 음수가 될 겁니다.
하지만 이 메서드에 숨겨진 요령이 있다면 반환된 인덱스 값의 비트를 뒤집어서 배열에서 가장 가까운 일치 값의 인덱스를 얻을 수 있다는 겁니다.
해당 값을 고정해서 범위 내에 있게 하면 됩니다.
이제 x 좌표가 탐색기의 x 좌표와 가장 가까운 타겟의 인덱스를 알아냈지만 타겟을 위아래로 검색하여 탐색기와 더욱 가까운 타겟이 존재하지 않는지 확인합니다.
이 검색에서 중요한 요령은 x 좌표값의 차이가 지금까지 찾아낸 최단 거리보다 더 클 경우 검색을 중단할 수 있다는 겁니다.
TargetPositions가 x 좌표에 따라 정렬되니까요
이 임곗값을 넘고 나면 해당 임곗값 반대편에 존재하는 모든 후보들은 우리가 이미 찾아낸 후보보다 더 가까이에 있을 수 없습니다.



핑백: DOTS 정리 (3) – HelloCube로 엔티티 알아보기 - 어제와 내일의 나 그 사이의 이야기