소수 구하기

https://www.acmicpc.net/problem/1929

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
2 초	256 MB	218115	61754	43484	26.573%

문제

M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다.

(1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.

출력

한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.

예제 입력 1

3 16

예제 출력 1

3
5
7
11
13

출처

• 데이터를 추가한 사람: jinjean0123, yongjun042

알고리즘 분류

• 수학
• 정수론
• 소수 판정
• 에라토스테네스의 체

---

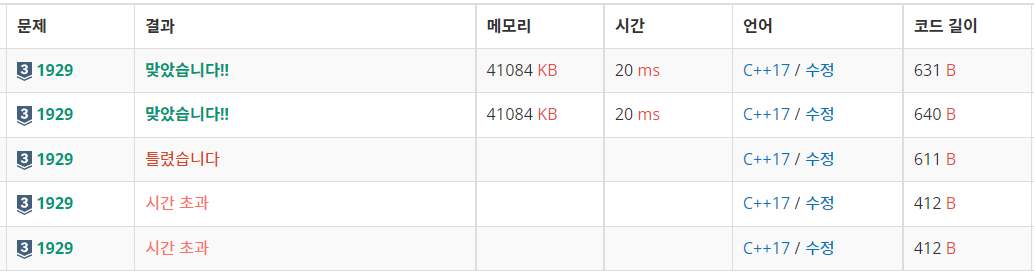
틀린 코드 (시간 초과)

소수는 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수다.

따라서 2부터 판별하는 수 전까지 나눠보고 나머지가 0이 안나온다면 소수로 정의한다.

여기에 더해서 해당 수보다 절반 이후의 숫자들은 확인이 필요 없는 숫자이므로

코드에 적용하여 제출하였으나 시간 초과….

#include <iostream>
#include <list>

using namespace std;

int arr[2];

int temp;

list<int> myList;

int main()
{
	cin >> arr[0] >> arr[1];

	for (int i = arr[0]; i <= arr[1]; i++) {
		temp = i;
		for (int j = 2; j <= temp/2; j++) {
			if (temp % j == 0) break;
			else if (j == temp/2) cout << temp << "\n";
		}
	}

	//for (auto it = myList.begin(); it != myList.end(); it++) cout << *it << "\n";

	return 0;
}

이것 저것 시도를 해보다가 소수를 찾는 방법 중에서 효율적인 방법인 ‘에라토스테네스의 체’ 를 알게 되었다.

https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4

‘에라토스테네스의 체’ 알고리즘

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
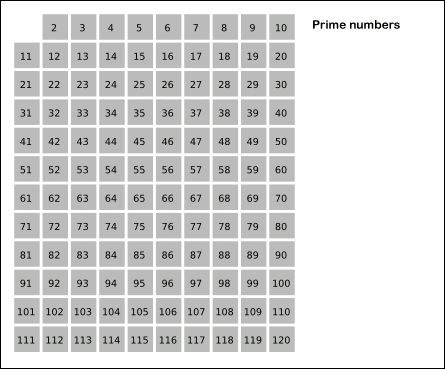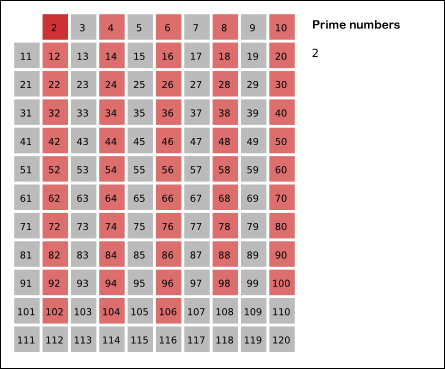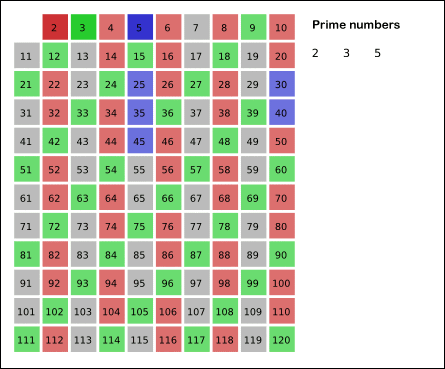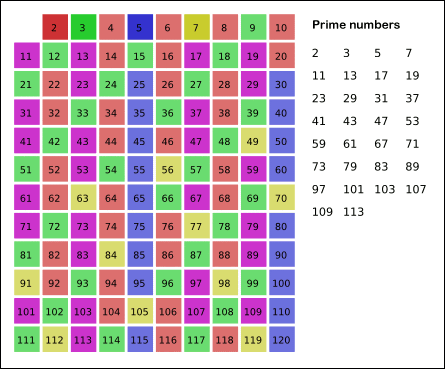
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.

그림의 경우,  11^2 < 120 이므로 11보다 작은 수의 배수들만 지워도 충분하다.

즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

에라토스테네스의 체를 프로그래밍 언어로 구현

void Eratos(int n)
{
    /*  만일 n이 1보다 작거나 같으면 함수 종료 */
    if (n <= 1) return;

    /*	2부터 n까지 n-1개를 저장할 수 있는 배열 할당
		배열 참조 번호와 소수와 일치하도록 배열의 크기는
		n+1 길이만큼 할당(인덱스 번호 0과 1은 사용하지 않음)	*/
	bool* PrimeArray = new bool[n + 1];

	/*  배열초기화: 처음엔 모두 소수로 보고 true값을 줌	*/
	for (int i = 2; i <= n; i++)
	    PrimeArray[i] = true;

	/*	에라토스테네스의 체에 맞게 소수를 구함
		만일, PrimeArray[i]가 true이면 i 이후의 i 배수는 약수로 i를
		가지고 있는 것이 되므로 i 이후의 i 배수에 대해 false값을 준다.
		PrimeArray[i]가 false이면 i는 이미 소수가 아니므로 i의 배수 역시
		소수가 아니게 된다. 그러므로 검사할 필요도 없다.
또한 i*k (k < i) 까지는 이미 검사되었으므로 j시작 값은 i*2에서 i*i로 개선할 수 있다.
	*/
	for (int i = 2; i * i <= n; i++)
	{
		if (PrimeArray[i])
			for (int j = i * i; j <= n; j += i)
			    PrimeArray[j] = false;
	}

	// 이후의 작업 ...
}

통과된 코드

#include <iostream>
#include <cmath>

using namespace std;

int M, N, temp;

int arr[10000001];

int main()
{
	cin >> M >> N;

	temp = sqrt(N);
	arr[0] = 0;
	arr[1] = 0;

	// 배열 초기화
	for (int i = 2; i <= N; i++) {
		arr[i] = i;
	}

	for (int i = 2; i <= temp; i++) {

		// 값이 0 이라는 뜻은 '지워진 수' 라는 의미
		if (arr[i] == 0) continue;

		// 이미 지워진 숫자가 아니라면, 
		// 그 배수부터 출발하여, 가능한 모든 숫자 지우기
		for (int j = 2 * i; j <= N; j += i) {
			arr[j] = 0;
		}
	}

	for (int i = M; i <= N; i++) {

		if (arr[i] == 0) continue;
		else cout << arr[i] << "\n";
	}

	return 0;
}

갈 길이 멀당