특정한 최단 경로
https://www.acmicpc.net/problem/1504
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 256 MB | 61021 | 15491 | 10492 | 24.539% |
문제
방향성이 없는 그래프가 주어진다. 세준이는 1번 정점에서 N번 정점으로 최단 거리로 이동하려고 한다.
또한 세준이는 두 가지 조건을 만족하면서 이동하는 특정한 최단 경로를 구하고 싶은데,
그것은 바로 임의로 주어진 두 정점은 반드시 통과해야 한다는 것이다.
세준이는 한번 이동했던 정점은 물론, 한번 이동했던 간선도 다시 이동할 수 있다.
하지만 반드시 최단 경로로 이동해야 한다는 사실에 주의하라.
1번 정점에서 N번 정점으로 이동할 때, 주어진 두 정점을 반드시 거치면서 최단 경로로 이동하는 프로그램을 작성하시오.
입력
첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000)
둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데,
a번 정점에서 b번 정점까지 양방향 길이 존재하며, 그 거리가 c라는 뜻이다. (1 ≤ c ≤ 1,000)
다음 줄에는 반드시 거쳐야 하는 두 개의 서로 다른 정점 번호 v1과 v2가 주어진다. (v1 ≠ v2, v1 ≠ N, v2 ≠ 1)
임의의 두 정점 u와 v사이에는 간선이 최대 1개 존재한다.
출력
첫째 줄에 두 개의 정점을 지나는 최단 경로의 길이를 출력한다.
그러한 경로가 없을 때에는 -1을 출력한다.
예제 입력 1
4 6 1 2 3 2 3 3 3 4 1 1 3 5 2 4 5 1 4 4 2 3
예제 출력 1
7
예제 입력 A
2 0 1 2
예제 출력 A
-1
예제 입력 B
4 6 1 2 10 2 3 10 4 3 1 4 1 1 1 3 10 4 2 2 2 3
예제 출력 B
7
예제 입력 C
800 3 1 800 4 800 2 2 3 800 6 2 3
예제 출력 C
20
예제 입력 D
800 3 2 1 2 1 800 3 800 4 1 2 4
예제 출력 D
9
예제 입력 E
4 2 1 2 1 2 3 1 2 3
예제 출력 E
-1
출처
- 데이터를 추가한 사람: alex9801, paldad, rhdqor213
- 문제의 오타를 찾은 사람: ZZangZZang
알고리즘 분류
통과된 코드 1 (비효율)
모든 배열을 선언해서 메모리 부분에서 꽝
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
constexpr int MAXN = 8001;
constexpr int INF = INT32_MAX;
// Dijkstra 알고리즘에 사용할 우선순위 큐
priority_queue<pair<int, int>> myPQ;
///*
//각 노드에 연결되어 있는 노드에 대한 정보를 담는 벡터
//a번 노드에서 b번 노드로 가는 비용이 c라는 의미
//graph[a].push_back((make_pair(B, C));
//*/
vector<pair<int, int>> graph[MAXN];
// dist[i][j]
// => i 에서 j 까지의 최단거리 (임시 노드)
int disArr[MAXN][MAXN];
// N : 정점의 개수, E : 간선의 개수
// U: 현재 노드, V : 이웃 노드, dist : 거리
// V1, V2 필수 정점
int N, E, U, V, dist, V1, V2;
int result = 0;
void Dijkstra(int start)
{
// 임시배열 초기화
for (int i = 1; i <= N; i++) disArr[start][i] = INF;
// 우선순위 큐에 삽입.
myPQ.push({ 0, start }); // < first : 거리 , second : 노드 인덱스 >
disArr[start][start] = 0;
while (!myPQ.empty()) {
// -를 붙이는 이유는 우선순위 큐를 이용하여 정렬하기 위함이다.
// (최소힙으로 구현)
int nCost = -myPQ.top().first;
int now = myPQ.top().second;
myPQ.pop();
// 해당 노드에서 연결된 모든 경로를 확인
for (int i = 0; i < graph[now].size(); i++) {
// 0이라면 길이 없다는 의미 continue
if (graph[now][i].second == 0) continue;
// disSum = 임시 노드 + 현재 노드에서 i로가는 비용
int disSum = nCost + graph[now][i].second;
// 비용이 더 작다면 최단경로 테이블 값을 갱신.
if (disSum < disArr[start][graph[now][i].first]) {
// 임시 노드 업데이트
disArr[start][graph[now][i].first] = disSum;
// 우선순위 큐에 (거리, 노드 인덱스) 푸시
myPQ.push(make_pair(-disSum, graph[now][i].first));
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
cin.tie(NULL);
cout.tie(NULL);
// N 정점의 개수, E 간선의 개수를 입력받는다.
cin >> N >> E;
for (int i = 0; i < E; i++) {
cin >> U >> V >> dist;
graph[U].push_back(make_pair(V, dist));
graph[V].push_back(make_pair(U, dist)); // 역방향
}
// V1, V2 필수 정점을 입력받는다.
cin >> V1 >> V2;
Dijkstra(1);
Dijkstra(V1);
Dijkstra(V2);
Dijkstra(N);
// 1 -> V1 -> V2 -> N 과 1 -> V2 -> V1 -> N 을 비교
result = min(disArr[1][V2] + disArr[V2][V1] + disArr[V1][N], disArr[1][V1] + disArr[V1][V2] + disArr[V2][N]);
// 1 -> N 으로 가는 경우 또는
if (disArr[1][N] == INF || disArr[V1][V2] == INF) cout << -1;
else cout << result;
return 0;
}
메모리 제한이 256MB인데 255.968MB…
동적으로 만들고 싶지 않아서 나올 수 있는 경우의 배열을 전부 선언해서 그런 것 같다.
1 -> V1 -> V2 -> N 과 1 -> V2 -> V1 -> N 을 비교를 생각 못해서 계속 틀렸다.
통과된 코드 2
생각해보니 N에서는 Dijkstra 알고리즘을 사용할 필요가 없다. => 제거 (약간의 속도 상승)
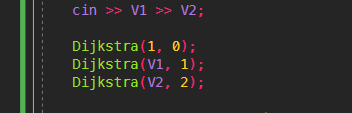
배열로 모든 간선을 미리 선언해두면 낭비 => 불필요한 배열 제거 (이곳에서 큰 차이가 난다.)
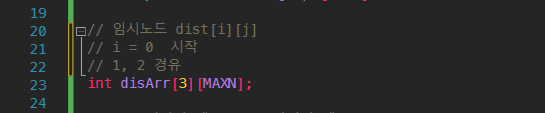
위의 변경사항으로 함수도 수정
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
constexpr int MAXN = 8001;
constexpr int INF = INT32_MAX;
// Dijkstra 알고리즘에 사용할 우선순위 큐
priority_queue<pair<int, int>> myPQ;
///*
//각 노드에 연결되어 있는 노드에 대한 정보를 담는 벡터
//a번 노드에서 b번 노드로 가는 비용이 c라는 의미
//graph[a].push_back((make_pair(B, C));
//*/
vector<pair<int, int>> graph[MAXN];
// 임시노드 dist[i][j]
// i = 0 시작
// 1, 2 경유
int disArr[3][MAXN];
// N : 정점의 개수, E : 간선의 개수
// U: 현재 노드, V : 이웃 노드, dist : 거리
// V1, V2 필수 정점
int N, E, U, V, dist, V1, V2;
int result = 0;
void Dijkstra(int start, int number)
{
// 임시배열 초기화
for (int i = 1; i <= N; i++) disArr[number][i] = INF;
// 우선순위 큐에 삽입.
myPQ.push({ 0, start }); // < first : 거리 , second : 노드 인덱스 >
disArr[number][start] = 0;
while (!myPQ.empty()) {
// -를 붙이는 이유는 우선순위 큐를 이용하여 정렬하기 위함이다.
// (최소힙으로 구현)
int nCost = -myPQ.top().first;
int now = myPQ.top().second;
myPQ.pop();
// 해당 노드에서 연결된 모든 경로를 확인
for (int i = 0; i < graph[now].size(); i++) {
// 0이라면 길이 없다는 의미 continue
if (graph[now][i].second == 0) continue;
// disSum = 임시 노드 + 현재 노드에서 i로가는 비용
int disSum = nCost + graph[now][i].second;
// 비용이 더 작다면 최단경로 테이블 값을 갱신.
if (disSum < disArr[number][graph[now][i].first]) {
// 임시 노드 업데이트
disArr[number][graph[now][i].first] = disSum;
// 우선순위 큐에 (거리, 노드 인덱스) 푸시
myPQ.push(make_pair(-disSum, graph[now][i].first));
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
cin.tie(NULL);
cout.tie(NULL);
// N 정점의 개수, E 간선의 개수를 입력받는다.
cin >> N >> E;
for (int i = 0; i < E; i++) {
cin >> U >> V >> dist;
graph[U].push_back(make_pair(V, dist));
graph[V].push_back(make_pair(U, dist)); // 역방향
}
// V1, V2 필수 정점을 입력받는다.
cin >> V1 >> V2;
Dijkstra(1, 0);
Dijkstra(V1, 1);
Dijkstra(V2, 2);
// 1 -> V1 -> V2 -> N 과 1 -> V2 -> V1 -> N 을 비교
result = min(disArr[0][V2] + disArr[2][V1] + disArr[1][N], disArr[0][V1] + disArr[1][V2] + disArr[2][N]);
// 1 -> N 으로 가는 경우 또는
if (disArr[0][N] == INF || disArr[1][V2] == INF) cout << -1;
else cout << result;
return 0;
}
아주 성공적이다 .
엄청난 메모리 차이를 보여준다.
![백준 1799번 (비숍, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)
![Programmers 72414 광고 삽입 [2021 KAKAO BLIND RECRUITMENT]](https://lycos7560.com/wp-content/uploads/2023/03/programmers.jpg)
![백준 11720번 (숫자의 합, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/2022/10/boj-og-1-2048x1070-1-1024x535.png)
![백준 2178번 (미로 탐색, C++, BFS) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og-1.png)
핑백: 백준 1753번 (최단경로, C++, Dijkstra) [BAEKJOON] - 어제와 내일의 나 그 사이의 이야기