요약
a>b인 두 양의 정수 a,b에 대하여,
a=qb+r(나머지 r은 0 이상 b 미만,q는 몫) 이라 하면,
gcd(a,b)=gcd(b,r)
( a , b 의 최대공약수 = b, r 의 최대공약수 )이다
최소 공배수 = ( a x b ) / GCD
시간 복잡도 : O(logN)
최대 공약수 (gcd)
int gcd(int a, int b) { // Greatest Common Divisor
return b ? gcd(b, a%b) : a;
}
int gcd(int a, int b) { // Greatest Common Divisor
int c;
while (b) {
c = a % b;
a = b;
b = c;
}
return a;
}
최소 공배수 (lcm)
int lcm(int a, int b) { // Least Common Muliple
return a * b / gcd(a, b);
}
알고리즘 – 유클리드 호제법(Euclidean Algorithm)
https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95
최대 공약수 (Greatest Common Divisor, GCD)
두 자연수의 공통된 약수 중에서 가장 큰 수
클리드 호제법 또는 유클리드 알고리즘은 가장 오래된 알고리즘으로
2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘의 하나이다.
호제법이란 말은 두 수가 서로 상대방 수를 나누어서 결국 원하는 수를 얻는 알고리즘을 나타낸다.
2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b),
a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
이 성질에 따라, b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나눈 나머지를 구하는 과정을 반복하여
나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.
이는 명시적으로 기술된 가장 오래된 알고리즘으로서도 알려져 있으며,
기원전 300년경에 쓰인 《원론》 제7권, 명제 1부터 3까지에 해당한다.
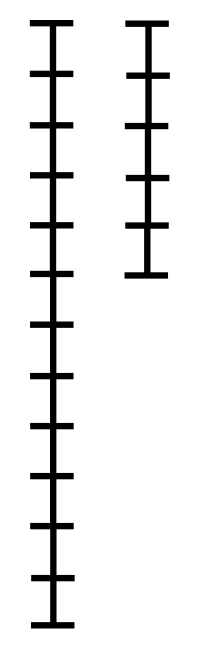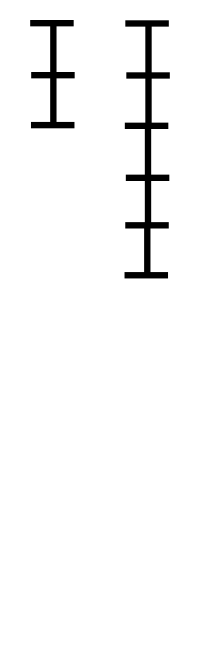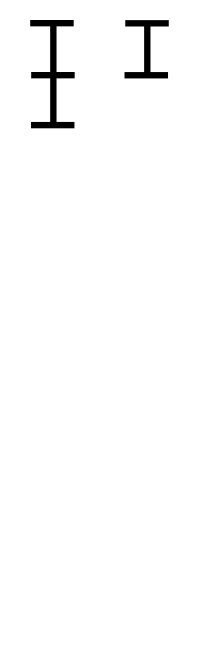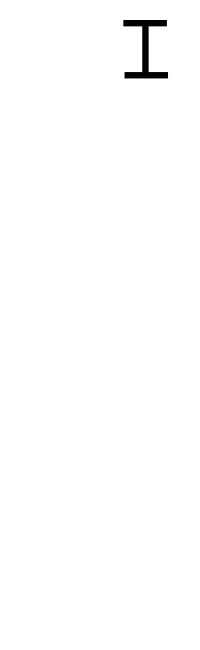
예시 및 코드
1071과 1029의 최대공약수를 구하면,
1071은 1029로 나누어 떨어지지 않기 때문에, 1071을 1029로 나눈 나머지를 구한다. ≫ 42
1029는 42로 나누어 떨어지지 않기 때문에, 1029를 42로 나눈 나머지를 구한다. ≫ 21
42는 21로 나누어 떨어진다.
따라서, 최대공약수는 21이다.
78696과 19332의 최대공약수를 구하면,
78696 = 19332×4 + 1368 19332 = 1368×14 + 180 1368 = 180×7 + 108 180 = 108×1 + 72 108 = 72×1 + 36 72 = 36×2 + 0
따라서, 최대공약수는 36이다.
시간 복잡도 : O(logN)
int gcd(int a, int b) { // 숏코딩, Greatest Common Divisor
return b ? gcd(b, a%b) : a;
}
int gcd(int a, int b) { // Greatest Common Divisor
int c;
while (b) {
c = a % b;
a = b;
b = c;
}
return a;
}
증명

+ 최소 공배수 (Least Common Muliple, LCM)
두 자연수의 공통된 배수 중 가장 작은 수
최소 공배수 = 두 자연수의 곱 / 최대 공약수 ( LCM = a x b / GCD )
int lcm(int a, int b) { // Least Common Muliple
return a * b / gcd(a, b);
}





핑백: 백준 2609번 (최대공약수와 최소공배수, C++) [BAEKJOON] - 어제와 내일의 나 그 사이의 이야기