비둘기 집의 원리

---

n+1개의 물건을 n개의 상자에 넣은 경우, 최소한 한 상자에는 그 물건이 반드시 두 개 이상 들어있다는 원리를 말한다.

보통 비둘기와 비둘기집의 형태로 비유되어 쓰이기 때문에, 비둘기 집의 원리라고 불린다.

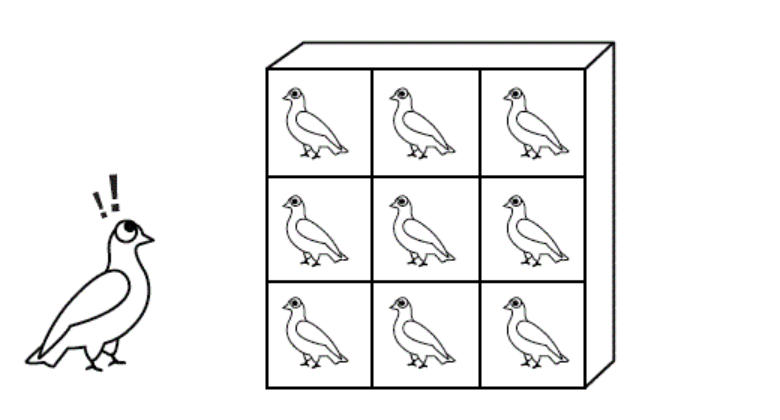
비둘기가 10마리, 집이 9개라면 한마리가 남는다.

증명

---

간단한 귀류법으로 증명할 수 있다.

모든 비둘기가 집에 들어간다는 가정 하에

개의 비둘기집과 마리의 비둘기가 있다고 가정한다.
만약 각 비둘기집에 한 마리 이하의 비둘기만 들어 있다면, 전체 비둘기집에는 많아야 마리의 비둘기가 존재한다.
그런데 비둘기는 모두 마리이므로, 이것은 모순이다.
따라서 어느 비둘기집에는 두 마리 이상의 비둘기가 있다.

이 증명은 대표적인 존재증명이다.

즉, 비둘기가 두 마리 이상 존재하는 집이 정확히 어떤 집인지는 이 증명으로 알아낼 수 없다.

비둘기집의 원리의 일반화

---

일반화된 비둘기집 원리는 다음과 같다.

개의 별개의 사물을 개의 용기에 나누어 담으면 적어도 한 개의 용기는  이상의 사물을 담고 있어야 한다.

(여기서, 는 보다 작지 않은 최소 정수를 의미한다.)

확률론적으로 일반화된 비둘기집 원리는 다음과 같다.

의 균일한 확률로 개의 비둘기를 무작위로 개의 비둘기집에 넣었다면 확률적으로 적어도 하나의 비둘기집에 두마리 이상의 비둘기가 들어가게 된다.

 인 경우와, 인 경우(단, )에 확률은 0인데, 달리 말하면 비둘기가 한마리 밖에 없다고 하면,

충돌(한 비둘기집에 두 마리 이상의 비둘기가 들어가는 일)이 일어날 수 없다는 것이다. 

 (비둘기가 비둘기집보다 많다)이라면 확률은 1이 되고 이런 경우에는 보통의 비둘기집 원리와 같은 일이 일어난다.

그러나 비둘기의 수가 비둘기집의 수를 초과하지 않는다 하더라도 (), 비둘기 분배의 무작위적인 성질에 의하여 종종 상당한 확률로 충돌이 일어난다.

예를 들어, 2마리의 비둘기가 무작위로 4개의 비둘기집에 분배된다면, 25%의 확률로 적어도 하나의 비둘기집에 두마리 이상의 비둘기가 들어가게 될 것이며,

5마리의 비둘기를 10개의 비둘기집에 분배한다면 확률은 69.76%가 되고, 10마리의 비둘기를 20개의 비둘기집에 분배하면 그 확률은 약 93.45%가 된다.

출처 : https://ko.wikipedia.org/wiki/%EB%B9%84%EB%91%98%EA%B8%B0%EC%A7%91_%EC%9B%90%EB%A6%AC

관련 문제

---

백준 20529번 가장 가까운 세 사람의 심리적 거리

https://www.acmicpc.net/problem/20529

백준 20529번 (가장 가까운 세 사람의 심리적 거리, C++) [BAEKJOON]

백준 비둘기 집의 원리 관련 문제들

https://www.acmicpc.net/problemset?sort=ac_desc&algo=189