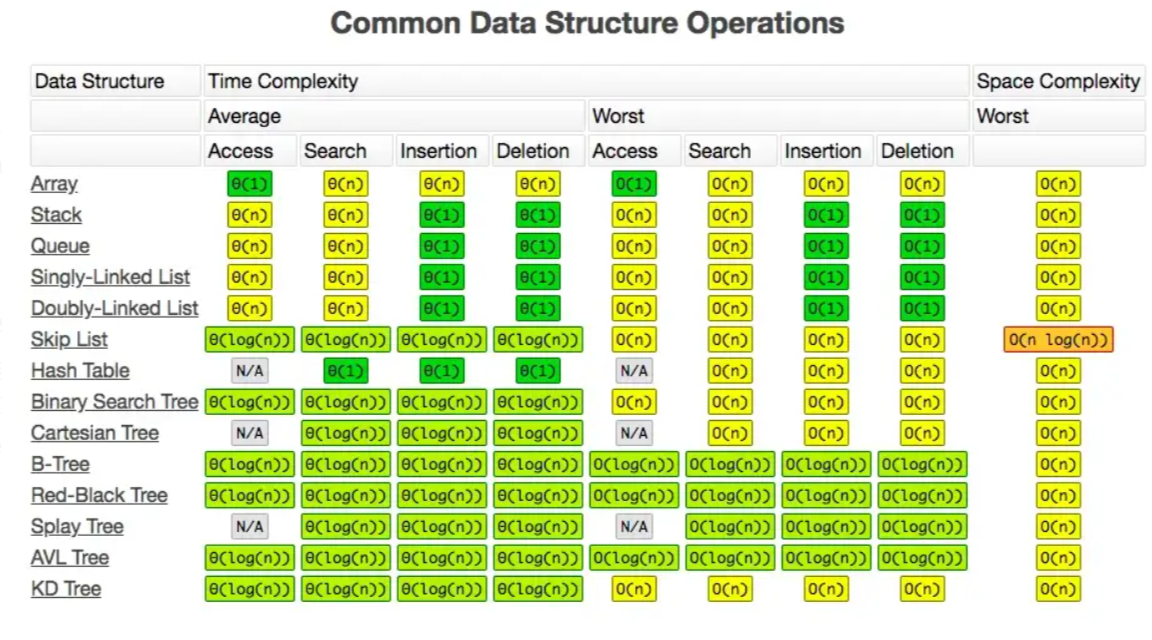
시간 복잡도 / 공간 복잡도
상황에 맞는 좋은 알고리즘을 선택하기 위해서는 알고리즘의 효율성을 확인해야 한다.
이 때 효율성 측정에는 시간 복잡도(time complexity)와 공간 복잡도(space complexity)라는 두 부분이 있다.
시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계
공간 복잡도는 문제를 해결하는데 필요로 하는 자원 공간의 양
Big-O 표기법 (Big-O Notation)
시간 복잡도의 표기법은
최선 경우 분석(Best Case Analysis) => Big-Ω(빅-오메가) / 하한 점근
-> 알고리즘 최상의 실행 시간을 표기한다.
최악 경우 분석(Worst Case Analysis) => Big-O(빅-오) / 상한 점근
-> 알고리즘 최악의 실행 시간을 표기한다.
평균 경우 분석(Average Case Analysis) => Big-θ(빅-세타) / 그 둘의 평균
-> 알고리즘 평균 실행 시간을 표기한다.
일반적으로 위의 3가지 경우로 분류한다.
그중에서 Big-O 표기법은 최소한 보장되는 성능을 표기하기 때문에 가장 많이 사용하는 표기법이다.
(불확실성을 제거하기 위해 최악의 경우를 사용)
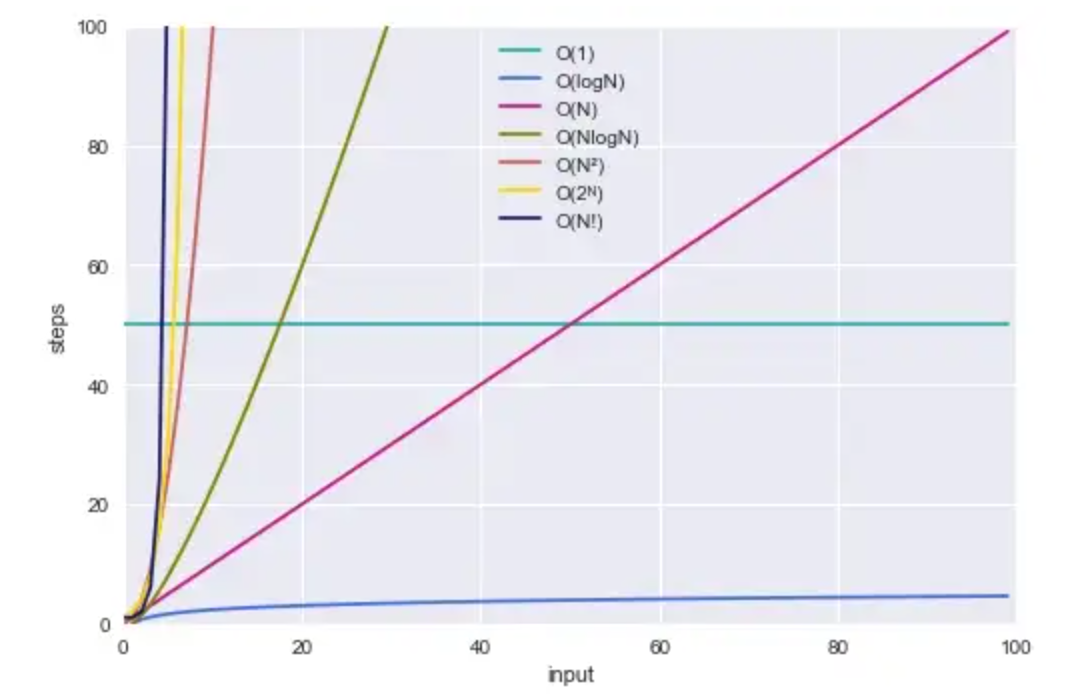
O(1) < O(logN) < O(N) < O(N logN) < O(N²) < O(2ᴺ) < O(N!)
O(1) – 상수 시간 (Constant Time)
입력한 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘
O(1) 알고리즘은 데이터(data)가 증가해도, 처리속도(time)에는 변함이 없는 알고리즘이다.
#include <iostream>
using namespace std;
int main()
{
cout << "Do Something!!";
return 0;
}
#include <iostream>
using namespace std;
int main()
{
cout << "Do Something!!";
cout << "Do Something!!";
return 0;
}
두번 출력을 하는 코드는 O(2)가 아닌 O(1)이다.
왜냐하면 Big O는 함수의 디테일에는 관심이 없기 때문이다.
그저 input 사이즈에 따라서 달라진다.

O(N) – 선형 시간 (Linear Time)
O(N)는 완벽한 대각선
최악의 경우에 n번의 연산을 수행해야 하는 알고리즘으로 데이터가 추가될 때마다 알고리즘이 한 단계 더 진행된다.
이것이 선형 시간이라고 하는 이유
ex) 1중 for문
#include <iostream>
using namespace std;
int main()
{
int N = 0;
cin >> N;
for (int i = 0; i < N; i++) {
cout << "Do Something!!" << "\n";
}
return 0;
}
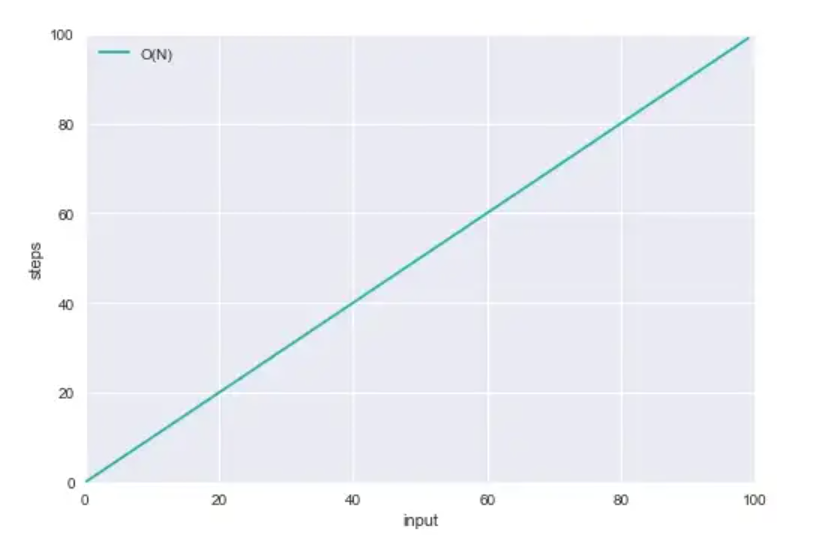
* 참고 * O(1) / O(N)
O(1)과 O(N)의 알고리즘으로 같은 문제를 50까지 수행한다면
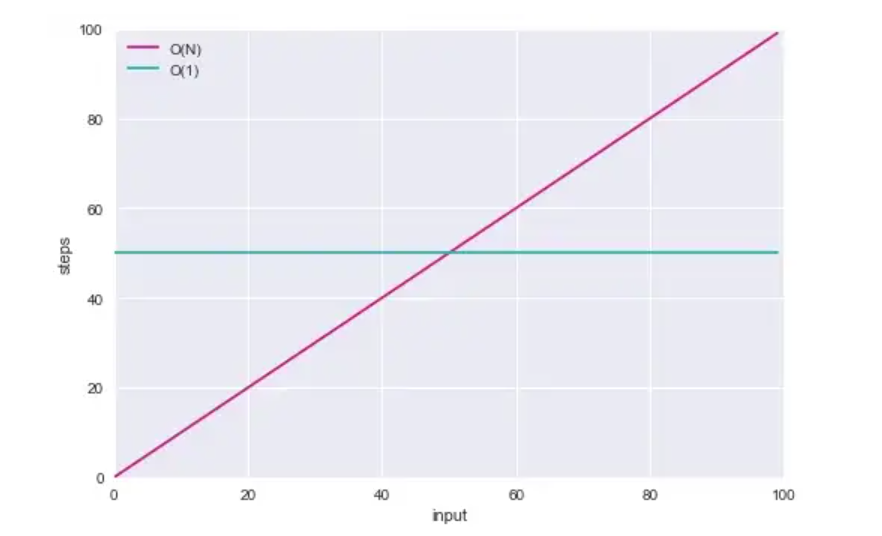
→ 입력 배열의 요소가 50개 미만일 때 O(N)가 더 효율적
→ 정확히 50개의 요소에서 두 알고리즘은 동일한 단계 수를 사용
→ 데이터가 증가할수록 O(N)더 많은 단계가 필요
Big-O 표기법은 데이터가 무한대로 커짐에 따라 알고리즘이 어떻게 수행되는지 살펴보기 때문에
O(N)가 보다 덜 효율적인 것으로 간주되는 이유다.
O(N²) – 2차 시간 (Quadratic Time)
성능이 입력 요소 크기의 제곱에 비례하는 알고리즘의 복잡성을 나타낸다. 일반적으로 매우 느리다.
주로 중첩 반복이 있을 때 발생하게 된다.
루프안에서 루프가 실행된다면, 20개의 데이터는 400개의 스텝이 된다. O(n^2)
ex) 2중 for문, 삽입(Insertion)/거품(Bubble)/선택(Selection) 정렬 등…
#include <iostream>
using namespace std;
int main()
{
int N = 0;
cin >> N;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cout << "Do Something!!" << "\n";
}
}
return 0;
}

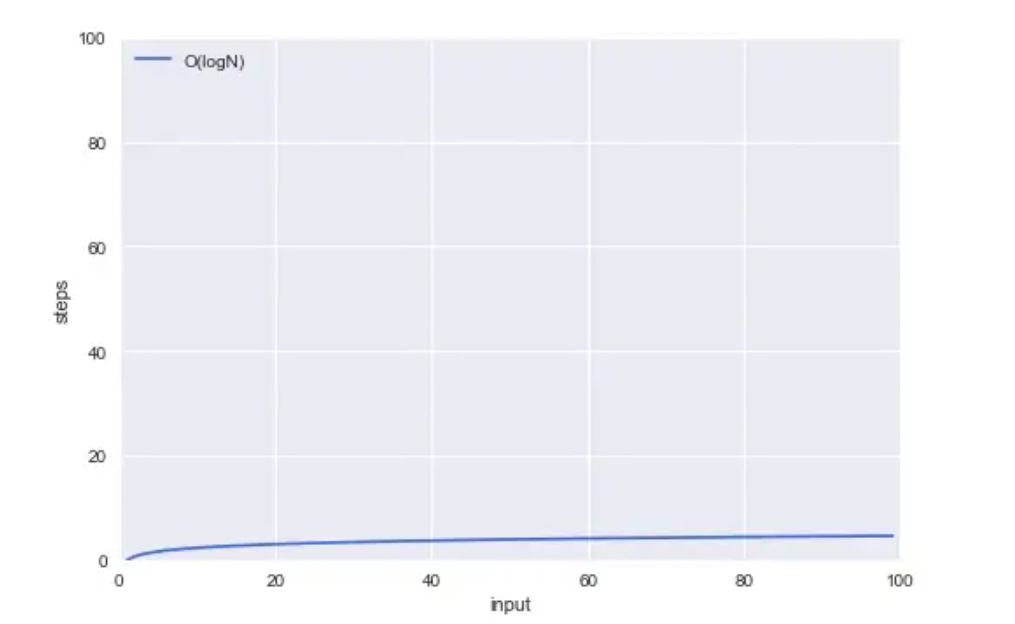
O(logN) – 로그 시간 (Logarithmic Time)
연산이 한 번 실행될 때 마다 데이터의 크기가 절반 감소하는 알고리즘 (log의 지수는 항상 2)
데이터의 관점으로 말하면 O(logN)은 데이터가 두 배가 될 때마다 작업 수가 하나씩 증가한다.
ex) binary search 알고리즘, tree 형태 자료구조 탐색
// 이진 탐색
int BinarySearch(int arr[], int size, int target)
{
int low = 0;
int high = size - 1;
int mid = 0;
while (low <= high)
{
mid = (low + high) / 2;
if (target < arr[mid])
high = mid - 1;
else if (target > arr[mid])
low = mid + 1;
else
return mid; // 반환 값은 인덱스
}
return -1;
}
O(N logN) – 로그 선형 시간 (Log-linear Time)
O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태
log(N)작업 N시간을 수행
ex) 퀵(Quick) / 병합(Merge) / 힙(Heap) 정렬, 분할 정복 알고리즘
O(2ᴺ) – 지수 시간 (Exponential Time)
매우 느린 시간 복잡도로 주로 재귀적으로 수행하는 알고리즘이 이에 해당
ex) fibonacci 수열
// 피보나치 수열
int Fibonaci(int n){
if (n == 1) return 0;
else if (n == 2) return 1;
else return Fibo(n - 1) + Fibo(n - 2);
}
O(N!) – 계승 시간(Factorial Time)
입력 크기의 계승에 비례하는 실행 시간
가장 느린 알고리즘으로 입력 값이 조금만 커져도 계산이 어렵다. (답없다.)
빅오 표기법(big-O notation) 규칙
계수 법칙: 상수를 제거하라
계수 법칙은 단순히 입력 크기와 연관되지 않은 상수를 전부 무시하는 것이다
빅오에서 입력 크기가 클 때 계수를 무시할 수 있다
상수 k > 0 인 경우 f(n)이 O(g(n))이면, kf(n)은 O(g(n)이다. 이 말은 즉, 5f(n)과 f(n)이 모두 동일한 O(f(n))이라는 빅오 표기법을 지님을 의미한다
합의 법칙: 빅오를 더하라
합의 법칙은 시간 복잡도를 더할 수 있다는 것을 의미한다
f(n)이 O(h(n))이고 g(n)이 O(p(n))이라면 f(n)+g(n)은 O(h(n))+O(p(n))이다 이 때 주의해야할 점은 합의 법칙을 적용한 다음 계수 법칙을 적용해야한다는 점이다
곱의 법칙: 빅오를 곱하라
곱의 법칙은 빅오가 어떤 식으로 곱해지는지에 관한 것이다
f(n)이 O(h(n))이고 g(n)이 O(p(n))이면 f(n)g(n)은 O(h(n)p(n))이다
다항 법칙: 빅오의 k승
다항 법칙은 다항 시간 복잡도가 동일한 다항 차수를 지닌 빅오 표기법을 지님을 의미한다
f(n)이 k차 다항식이면 f(n)은 O(nᵏ)이다
쉽게 말해, 빅오 표기법은 제일 영향력 있는 것만 신경쓰겠다는 의미
(최고 차항을 남기고, 상수는 버린다)
O(30n³+20n²+500n+3000)로 표시된 값이 있을 때, 빅오 표기법은 제일 영향력 있는 것만 남겨 O(n³)으로만 표기한다
참고 사이트
https://towardsdatascience.com/introduction-to-big-o-notation-820d2e25d3fd
https://wing-beat.tistory.com/17
https://towardsdatascience.com/the-big-o-notation-d35d52f38134



핑백: 알고리즘 – 알고리즘 분석에 대한 정리 - 어제와 내일의 나 그 사이의 이야기