박스 채우기
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 128 MB | 4718 | 1271 | 909 | 27.224% |
문제
세준이는 length × width × height 크기의 박스를 가지고 있다.
그리고 세준이는 이 박스를 큐브를 이용해서 채우려고 한다.
큐브는 정육면체 모양이며, 한 변의 길이는 2의 제곱꼴이다.
(1×1×1, 2×2×2, 4×4×4, 8×8×8, …)
세준이가 가지고 있는 박스의 종류와 큐브의 종류와 개수가 주어졌을 때,
박스를 채우는데 필요한 큐브의 최소 개수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 세 자연수 length width height가 주어진다.
둘째 줄에 세준이가 가지고 있는 큐브의 종류의 개수 N이 주어진다.
셋째 줄부터 총 N개의 줄에 큐브의 종류 Ai와 개수 Bi가 i가 증가하는 순서대로 주어진다.
큐브의 종류는 한 변의 길이를 나타낼 때 쓰는 2i에서 i이다.
출력
첫째 줄에 필요한 큐브의 개수의 최솟값을 출력한다.
만약 채울 수 없다면 -1을 출력한다.
제한
- 1 ≤ length, width, height ≤ 106
- 1 ≤ n ≤ 20
- 0 ≤ Ai < 20
- 0 ≤ Bi ≤ 106
- Ai ≠ Aj (i ≠ j)
예제 입력 1
4 4 8 3 0 10 1 10 2 1
예제 출력 1
9
예제 입력 2
4 4 8 3 0 10 1 10 2 10
예제 출력 2
2
예제 입력 3
10 10 11 1 0 2000
예제 출력 3
1100
예제 입력 4
10 10 11 1 0 1099
예제 출력 4
-1
예제 입력 5
37 42 59 6 0 143821 1 14382 2 1438 3 143 4 14 5 1
예제 출력 5
5061
출처
알고리즘 분류
length × width × height 크기의 박스
이 박스를 큐브로 채우려고 한다.
큐브의 크기는 정육면체 모양이며 한 변의 길이는 2의 제곱 꼴 1, 2, 4, 8…
박스를 채우는데 필요한 큐브의 최소 개수를 찾는 문제
4 4 8 // 박스 length × width × height
3 // 큐브의 개수
0 10 // 변의 길이 : 2^0 10개 넓이 1 10개
1 10 // 변의 길이 : 2^1 10개 넓이 8 10개
2 1 // 변의 길이 : 2^2 1개 넓이 64 1개
넓이 128 64 + 10 + 10 + 10 + 10 + 10 + 10
박스는 부피
큐브는 각 큐브의 한 변의 길이와 개수만 가지고 있으면 될 것 같다
박스가 큐브의 개수와는 상관없이
만들어질 수 있는 경우의 수를 조건과 비교하면서 하면 어떨까???
입력 확인
#include <iostream>
#include <set>
using namespace std;
// 큐브의 변의 길이 순으로 내림차순 정렬
set<int, greater<int>> cubeSet;
set<int, greater<int>> ::iterator iter;
// 큐브의 개수를 저장 / 인덱스는 2^index
int cubeNumber[21] = { 0 };
// 박스의 가 세 높
int length, width, height = 0;
// 박스의 부피
int boxArea = 0;
// 큐브의 종류 , 큐브의 수
int type, Number = 0;
void Initializaion()
{
cin >> length >> width >> height;
boxArea = length * width * height;
int N = 0;
cin >> N;
while (N > 0)
{
cin >> type >> Number;
cubeSet.insert(type);
cubeNumber[type] += Number;
N--;
}
}
int main()
{
Initializaion();
cout << "박스의 부피 : " << boxArea << "\n";
for (iter = cubeSet.begin(); iter != cubeSet.end(); iter++)
{
cout << "큐브 변의 길이 2^ " << *iter << " 박스의 개수 : " << cubeNumber[*iter] << " \n";
}
return 0;
}
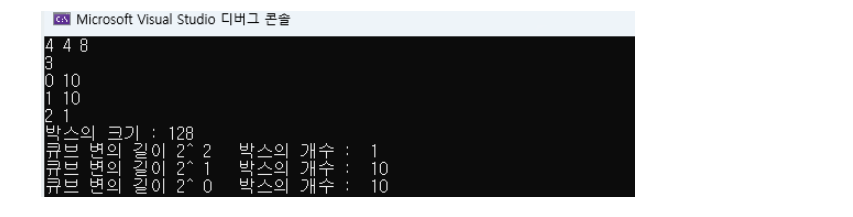
마지막 테스트 케이스에서 망… 함 ㅠ
부피로 접근하는 방법은 잘못된 방법이다
큐브들의 부피가 박스의 부피와 같다고 큐브가 박스 모양일 거라는 착각…
잘못된 로직과 코드 1
#include <iostream>
#include <set>
#include <cmath>
using namespace std;
// 큐브의 변의 길이 순으로 내림차순 정렬
set<int, greater<int>> cubeSet;
set<int, greater<int>> ::iterator iter;
// 큐브의 개수를 저장 / 인덱스는 2^index
int cubeNumber[21] = { 0 };
// 박스의 가 세 높
int length, width, height = 0;
// 박스의 넓이
int boxArea = 0;
// 큐브의 종류 , 큐브의 수
int type, Number = 0;
void Initializaion()
{
cin >> length >> width >> height;
boxArea = length * width * height;
int N = 0;
cin >> N;
while (N > 0)
{
cin >> type >> Number;
cubeSet.insert(type);
cubeNumber[type] += Number;
N--;
}
}
void CubeCheck(int cnt, int value)
{
if (value == boxArea)
{
cout << "찾았다 : " << cnt << " boxArea : " << boxArea << " value : " << value << "\n";
for (auto it = cubeSet.begin(); it != cubeSet.end(); it++)
{
cout << "it : " << *it << " cubeNumber[*it] : " << cubeNumber[*it] << "\n";
}
exit(0);
}
for (auto it = cubeSet.begin(); it != cubeSet.end(); it++)
{
if (cubeNumber[*it] == 0 || value > boxArea )
{
return;
}
//cout << "cubeNumber[" << *it << "] : " << cubeNumber[*it] << "\n";
cubeNumber[*it]--;
//cout << "cnt : " << cnt << " 들어갈 때 : " << value << " ";
CubeCheck(cnt + 1, value + pow(pow(2,*it),3));
cubeNumber[*it]++;
}
cout << -1;
exit(0);
}
int main()
{
Initializaion();
CubeCheck(0, 0);
return 0;
}
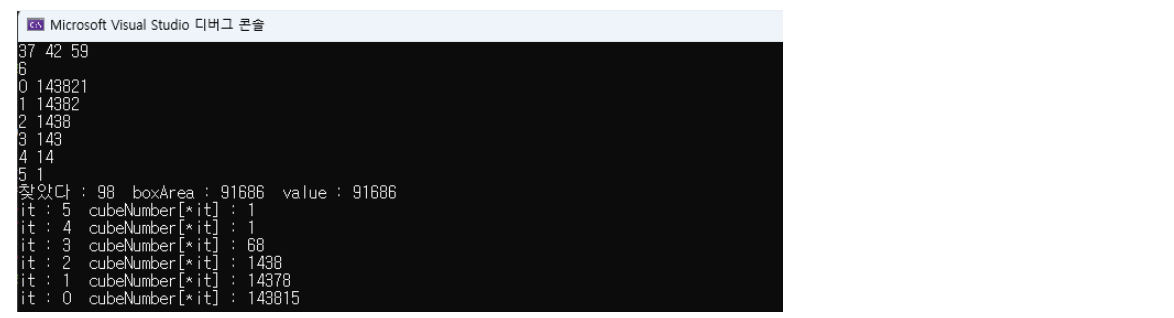
그렇다면 박스에서 접근해야 한다.
박스를 큐브의 규격을 기준으로 분할하여 그리디 알고리즘을 적용하면서 푸는 것 인가?
잘못된 로직과 코드 2
#include <iostream>
#include <set>
#include <cmath>
#include <algorithm>
using namespace std;
// 큐브의 변의 길이 순으로 내림차순 정렬
set<int, greater<int>> cubeSet;
set<int, greater<int>> ::iterator iter;
// 큐브의 개수를 저장 / 인덱스는 2^index
int cubeNumber[21] = { 0 };
int cubeNeedNumber[21] = { 0 };
// 박스의 X,Y,Z
int BoxXYZ[3] = { 0 };
int temp[3] = { 0 };
// 큐브의 종류 , 큐브의 수
int type, Number = 0;
int cubeCNT = 0;
void Initializaion()
{
cin >> BoxXYZ[0] >> BoxXYZ[1] >> BoxXYZ[2];
sort(BoxXYZ, BoxXYZ + (sizeof(BoxXYZ)/sizeof(BoxXYZ[0])));
int N = 0;
cin >> N;
while (N > 0)
{
cin >> type >> Number;
cubeSet.insert(type);
cubeNumber[type] += Number;
N--;
}
}
// 가장 큰 X를 기준으로 Z를 채워나감
// 들어오는 값은 X의 길이/Z의 남은 길이/ 몇번 나누었는지 확인(0부터 시작)
// 이 함수의 목적은 Z가 0이 될때까지 큐브를 찾는 것
void CubeCheckZ(int N, int leftZ, int divisionCount, int st)
{
for (;leftZ >= pow(2, N);)
{
cout << "leftZ : " << leftZ << " pow(2, N) : " << pow(2, N) << "\n";
if (divisionCount == 0 && st == pow(2, N))
{
BoxXYZ[2] -= st;
st = -1;
}
if (st == -1)
{
cubeNeedNumber[N] += pow(4, divisionCount);
}
else
{
cubeNeedNumber[N] += pow(4, divisionCount) * (st / pow(2, N));
}
leftZ -= pow(2, N);
if (leftZ == 0)
{
return;
}
}
// 남은 Z의 길이보다 pow(2, N)가 더 큰 상황
for (;leftZ < pow(2, N);)
{
N--;
divisionCount++;
cout << "남은 Z의 길이보다 작은 박스 값 찾기 : " << " N : " << N << " pow(2, N) : " << pow(2, N) << " leftZ : " << leftZ << "\n";
}
CubeCheckZ(N, leftZ, divisionCount, st);
}
// 박스 전체의 X길이와 Z의 길이
void CubeCheckX(int BoxX, int BoxZ, int st, int boxY)
{
if (BoxX == 0)
{
return;
}
// 처음 할 때
int N = 0;
for (int i = 0; i <= 20; i++)
{
if (boxY < pow(2, i))
{
N = i - 1;
break;
}
else if (boxY == pow(2, i))
{
N = i;
break;
}
//X의 값에 가장 근접한 2^i 를 구함
if (BoxX < pow(2, i) )
{
N = i - 1;
cout << "높을때 : " << N ;
//cubeNeedNumber[N]++;
break;
}
else if (BoxX == pow(2, i) )
{
//cout << "BoxX : " << BoxX << " 같을때" << N;
N = i;
//cubeNeedNumber[N]++;
break;
}
}
if (st <= pow(2,N))
{
st = pow(2, N);
}
// 박스의 Z길이보다 작거나 같은 2^N 의 N / 박스의 Z 길이
BoxX -= pow(2, N);
CubeCheckZ(N , BoxZ, 0, st);
cout << "BoxX : " << BoxX << "\n";
CubeCheckX(BoxX, BoxZ, st, boxY);
}
int main()
{
Initializaion();
for (;BoxXYZ[2] > 0;)
{
CubeCheckX(BoxXYZ[0], BoxXYZ[1], 0, BoxXYZ[2]);
cout << "BoxXYZ[2] : " << BoxXYZ[2] << "\n";
}
for (iter = cubeSet.begin(); iter != cubeSet.end(); iter++)
{
cout << "cubeNeedNumber[" << *iter << "] : " << cubeNeedNumber[*iter] << "\n";
}
return 0;
}
잘못된 로직과 코드 3
작성하다 보니 내가 왜 이렇게 작성했는지 이해할 수 없다.
#include <iostream>
#include <set>
#include <cmath>
#include <algorithm>
using namespace std;
set<int, greater<int>> cubeSet;
set<int, greater<int>> ::iterator iter;
int cubeNumber[21] = { 0 };
int cubeNeedNumber[21] = { 0 };
long long BoxXYZ[3] = { 0 };
int type, Number = 0;
void Initializaion()
{
cin >> BoxXYZ[0] >> BoxXYZ[1] >> BoxXYZ[2];
sort(BoxXYZ, BoxXYZ + (sizeof(BoxXYZ)/sizeof(BoxXYZ[0])));
int N = 0;
cin >> N;
while (N > 0)
{
cin >> type >> Number;
cubeSet.insert(type);
cubeNumber[type] += Number;
N--;
}
}
void CubeCheckZ(long long N, long long leftZ, long long divisionCount, long long MaxX, bool firstCheck)
{
for (;leftZ >= pow(2, N);)
{
if (MaxX == pow(2, N) || leftZ >= pow(2, N) && firstCheck)
{
if (N == 0)
{
cubeNeedNumber[N] += leftZ;
leftZ = 0;
continue;
}
cubeNeedNumber[N] += pow(4, divisionCount);
cout << "pow(4, divisionCount) : " << pow(4, divisionCount) << " divisionCount : " << divisionCount << " N : "<< N << "\n";
leftZ -= pow(2, N);
continue;
}
if (leftZ >= pow(2, N) && !firstCheck)
{
if (N == 0)
{
cubeNeedNumber[N] += leftZ * MaxX / pow(2, N);
leftZ = 0;
continue;
}
cubeNeedNumber[N] += MaxX / pow(2, N);
cout << "MaxX / pow(2, N) : " << MaxX / pow(2, N) << " " << MaxX << " / " << pow(2, N) << "\n";
leftZ -= pow(2, N);
}
}
if (leftZ == 0)
{
cout << "leftZ : " << leftZ << "\n";
return;
}
while(leftZ < pow(2, N))
{
N--;
divisionCount++;
}
CubeCheckZ(N, leftZ, divisionCount, MaxX, firstCheck);
}
void CubeCheckX(long long BoxX, long long BoxZ, long long MaxX, long long boxY, bool firstCheck)
{
if (BoxX == 0)
{
BoxXYZ[2] -= MaxX;
return;
}
int N = 0;
for (int i = 0; i <= 20; i++)
{
if (BoxX < pow(2, i) || (BoxXYZ[2] < pow(2, i)))
{
N = i - 1;
BoxX -= pow(2, N);
break;
}
else if (BoxX == pow(2, i) || (BoxXYZ[2] == pow(2, i)))
{
N = i;
BoxX -= pow(2, N);
break;
}
}
if (MaxX < pow(2,N))
{
MaxX = pow(2, N);
}
CubeCheckZ(N , BoxZ, 0, MaxX, firstCheck);
firstCheck = false;
CubeCheckX(BoxX , BoxZ, MaxX, boxY, firstCheck);
}
int main()
{
Initializaion();
while (BoxXYZ[2] != 0)
{
CubeCheckX(BoxXYZ[0], BoxXYZ[1], 0, BoxXYZ[2], true);
cout << BoxXYZ[2] << " \n";
}
for (iter = cubeSet.begin(); iter != cubeSet.end(); iter++)
{
cout << "cubeNeedNumber[" << *iter << "] : " << cubeNeedNumber[*iter] << "\n";
}
return 0;
}
통과된 코드
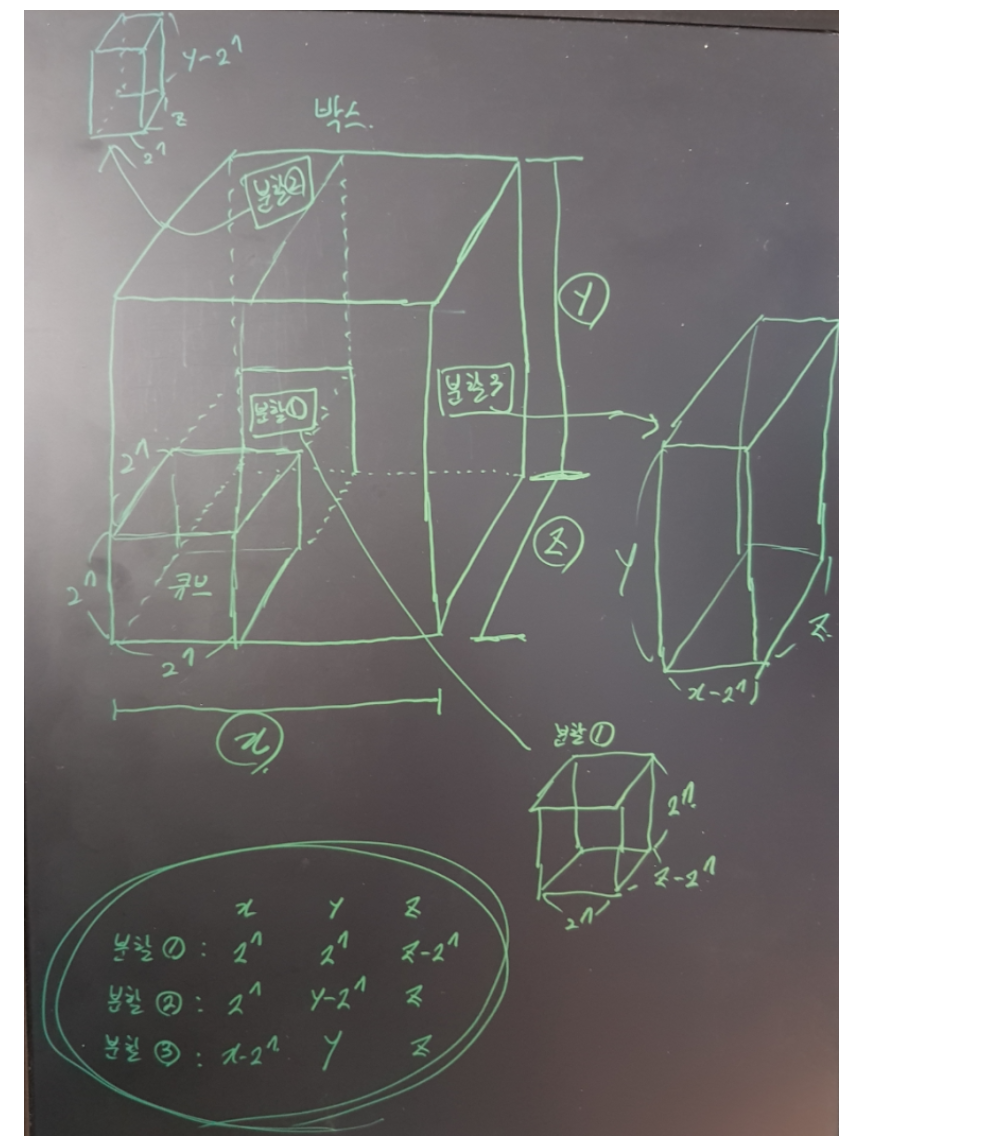
위와 같이 분할 된 박스를 다시 분할 X, Y, Z 가 0일 때까지
상자의 개수 조건에 부합하지 않으면 체크하고 -1 출력
#include <iostream>
#include <map>
#include <cmath>
using namespace std;
//cubeMultimap 은 내림차순으로 정렬된다.
multimap<int, int, greater<int>> cubeMultimap;
//cubeMultimap 순회를 위한 반복자
multimap<int, int, greater<int>>::iterator iter;
int length, width, height;
int numberOfCubes, cnt = 0;
int tempOne, tempTwo;
bool failCheck = false;
// 조건을 초기화 해주는 함수
void Initializaion()
{
cin >> length >> width >> height >> numberOfCubes;
while (numberOfCubes > 0)
{
cin >> tempOne >> tempTwo;
cubeMultimap.insert(make_pair(pow(2, tempOne), tempTwo));
numberOfCubes--;
}
}
// 분할 정복을 위한 함수 (X, Y, Z, 반복자)
void divisionConquest(int length, int width, int height, multimap<int, int, greater<int>>::iterator iter)
{
// 만약 X, Y, Z 중에서 0이 되는 값이 있다면 리턴
if (length == 0 || width == 0 || height == 0) return;
// 분할정복 로직부분
for (;iter != cubeMultimap.end(); iter++)
{
if (iter->second != 0 && length >= iter->first && width >= iter->first && height >= iter->first)
{
iter->second--;
cnt++;
divisionConquest(iter->first, iter->first, width - (iter->first), iter);
divisionConquest(length - iter->first, height, width, iter);
divisionConquest(height - iter->first, width, iter->first, iter);
return;
}
}
// 만약 큐브의 조건이 만족하지 않는다면 실패 마킹
failCheck = true;
return;
}
int main()
{
Initializaion();
// cubeMultimap의 가장 높은 값부터 시작
iter = cubeMultimap.begin();
divisionConquest(length, width, height, iter);
// 실패 마킹이 true 면 항상 -1 출력
if (failCheck) cout << -1;
else cout << cnt; // 아니면 큐브의 개수를 출력한다.
return 0;
}
분할 정복의 개념과 구현 방법은 몰라서 오래 고민한 문제
재귀 구현 어려웠다.
![백준 11005번 (진법 변환 2, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)
![백준 16928번 (뱀과 사다리 게임, C++, BFS) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/2022/10/boj-og-1-2048x1070-1-1024x535.png)