목차 테이블

거의 최단 경로
추가 예제
틀린 코드 (메모리 초과)
통과된 코드

거의 최단 경로

https://www.acmicpc.net/problem/5719

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
1 초	256 MB	23040	3945	2400	19.151%

문제

요즘 많은 자동차에서는 GPS 네비게이션 장비가 설치되어 있다.

네비게이션은 사용자가 입력한 출발점과 도착점 사이의 최단 경로를 검색해 준다.

하지만, 교통 상황을 고려하지 않고 최단 경로를 검색하는 경우에는 극심한 교통 정체를 경험할 수 있다.

상근이는 오직 자기 자신만 사용 가능한 네비게이션을 만들고 있다.

이 네비게이션은 절대로 최단 경로를 찾아주지 않는다. 항상 거의 최단 경로를 찾아준다.

거의 최단 경로란 최단 경로에 포함되지 않는 도로로만 이루어진 경로 중 가장 짧은 것을 말한다.

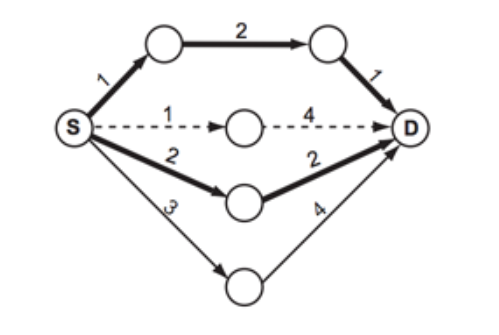
예를 들어, 도로 지도가 아래와 같을 때를 생각해보자.

원은 장소를 의미하고, 선은 단방향 도로를 나타낸다.

시작점은 S, 도착점은 D로 표시되어 있다. 굵은 선은 최단 경로를 나타낸다. (아래 그림에 최단 경로는 두 개가 있다)

거의 최단 경로는 점선으로 표시된 경로이다.

이 경로는 최단 경로에 포함되지 않은 도로로 이루어진 경로 중 가장 짧은 경로이다.

거의 최단 경로는 여러 개 존재할 수도 있다.

예를 들어, 아래 그림의 길이가 3인 도로의 길이가 1이라면, 거의 최단 경로는 두 개가 된다.

또, 거의 최단 경로가 없는 경우도 있다.

입력

입력은 여러 개의 테스트 케이스로 이루어져 있다.

각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 10⁴)가 주어진다.

장소는 0부터 N-1번까지 번호가 매겨져 있다. 둘째 줄에는 시작점 S와 도착점 D가 주어진다. (S ≠ D; 0 ≤ S, D < N)

다음 M개 줄에는 도로의 정보 U, V, P가 주어진다. (U ≠ V ; 0 ≤ U, V < N; 1 ≤ P ≤ 10³)

이 뜻은 U에서 V로 가는 도로의 길이가 P라는 뜻이다.

U에서 V로 가는 도로는 최대 한 개이다.

또, U에서 V로 가는 도로와 V에서 U로 가는 도로는 다른 도로이다.

입력의 마지막 줄에는 0이 두 개 주어진다.

출력

각 테스트 케이스에 대해서, 거의 최단 경로의 길이를 출력한다.

만약, 거의 최단 경로가 없는 경우에는 -1을 출력한다.

예제 출력 1

예제 입력 1

5
-1
6

출처

ICPC > Regionals > Latin America > South America Regional Contests 2008 A번

문제를 번역한 사람: baekjoon
데이터를 추가한 사람: gkswjdzz, sait2000, smsm8111
잘못된 데이터를 찾은 사람: tncks0121

알고리즘 분류

추가 예제

예제 출력 A

예제 출력 A

예제 입력 B

예제 출력 B

6
-1
-1
3

예제 입력 C

예제 출력 C

2
-1
-1
2

예제 입력 D

예제 출력 D

-1
3
2
-1

틀린 코드 (메모리 초과)

다익스트라의 경로를 저장하기 위하여 우선 순위 큐에 지나온 정점들을 list<pair<int, int>>에 담아 보았다.

당연하게 메모리 초과 (정답은 잘나온다… ㅜㅜ)

원리는 list에 있는 정점들을 방문처리하여 다음 다익스트라를 사용할 때 넘기는 방법을 사용했다.

#include <iostream>
#include <queue>
#include <vector>
#include <list>
#include <tuple>
#include <map>

using namespace std;

constexpr int INF = INT32_MAX;

int disArr[501];

bool check[501][501];

int N, M, S, D, U, V, P;

int Dijstra()
{
    int result = INF;

    for (int i = 0; i <= N; i++) {
        for (int j = 0; j <= N; j++) {
            check[i][j] = false;
        }
    }

    // 임시배열 초기화
    for (int i = 0; i <= N; i++) disArr[i] = INF;

    priority_queue<tuple<int, int, list<pair<int, int>>>> firstPQ;

    vector<pair<int, int>> graph[10000];

    list<pair<int, int>> myList;

    multimap<int, list<pair<int, int>>> myMap;

    for (int i = 0; i < M; i++) {
        cin >> U >> V >> P;
        graph[U].push_back(make_pair(V, P));
    }

    // 우선순위 큐에 삽입.
    firstPQ.push({ 0, S, myList }); // < first : 거리 , second : 노드 인덱스 >
    disArr[S] = 0;
    while (!firstPQ.empty()) {
        // -를 붙이는 이유는 우선순위 큐를 이용하여 정렬하기 위함이다.
        // (최소힙으로 구현)
        int nCost = -get<0>(firstPQ.top());
        int now = get<1>(firstPQ.top());
        myList = get<2>(firstPQ.top());
        firstPQ.pop();

        // 이미 담겨 있는 것보다 거리가 크면 넘어간다.
        if (disArr[now] < nCost) continue;

        // 해당 노드에서 연결된 모든 경로를 확인
        for (int i = 0; i < graph[now].size(); i++) {
            list<pair<int, int>> tempList = myList;
            // disSum = 임시 노드 + 현재 노드에서 i로가는 비용
            int disSum = nCost + graph[now][i].second;

            // 비용이 더 작다면 최단경로 테이블 값을 갱신.
            if (disSum <= disArr[graph[now][i].first]) {
                tempList.push_back(make_pair(now, graph[now][i].first));

                if (graph[now][i].first == D && result >= disSum) {
                    result = disSum;
                    myMap.insert(make_pair(disSum, tempList));
                }

                // 임시 노드 업데이트
                disArr[graph[now][i].first] = disSum;
                // 우선순위 큐에 (거리, 노드 인덱스) 푸시
                firstPQ.push(make_tuple(-disSum, graph[now][i].first, tempList));
            }
        }
    }

    result = disArr[D];

    for (auto mit = myMap.begin(); mit != myMap.end(); mit++) {
        if (result == mit->first) {
            for (auto it = mit->second.begin(); it != mit->second.end(); it++) {
                check[it->first][it->second] = true;
            }
        }

        else break;
    }

    priority_queue<pair<int, int>> myPQ;

    // 임시배열 초기화
    for (int i = 0; i <= N; i++) disArr[i] = INF;

    // 우선순위 큐에 삽입.
    myPQ.push({ 0, S }); // < first : 거리 , second : 노드 인덱스 >
    disArr[S] = 0;

    while (!myPQ.empty()) {
        // -를 붙이는 이유는 우선순위 큐를 이용하여 정렬하기 위함이다.
        // (최소힙으로 구현)
        int nCost = -myPQ.top().first;
        int now = myPQ.top().second;
        myPQ.pop();

        // 이미 담겨 있는 것보다 거리가 크면 넘어간다.
        if (disArr[now] < nCost) continue;
        // 해당 노드에서 연결된 모든 경로를 확인
        for (int i = 0; i < graph[now].size(); i++) {
            if (check[now][graph[now][i].first] == true) continue;
            // disSum = 임시 노드 + 현재 노드에서 i로가는 비용
            int disSum = nCost + graph[now][i].second;
            // 비용이 더 작다면 최단경로 테이블 값을 갱신.
            if (disSum <= disArr[graph[now][i].first]) {
                // 임시 노드 업데이트
                disArr[graph[now][i].first] = disSum;
                // 우선순위 큐에 (거리, 노드 인덱스) 푸시
                myPQ.push(make_pair(-disSum, graph[now][i].first));
            }
        }
    }

    return disArr[D];
}


int main()
{
    ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
    //cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
    cin.tie(NULL);
    std::cout.tie(NULL);

    while (true) {

        cin >> N >> M;

        if (N == 0 && M == 0) break;

        cin >> S >> D;

        int result = Dijstra();

        if (result == INF) cout << -1 << "\n";
        else cout << result << "\n";
    }



    return 0;
}

통과된 코드

vector<int> trace[501]; 를 이용하여 시작과 끝의 정점들을 넣어준다.

주의할 점은 도착지에서 출발지 방향으로 탐색을 하기 위해서 반대로 넣어주어야 한다.

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

constexpr int INF = INT32_MAX;

int disArr[501];

priority_queue<pair<int, int>> mypq;

vector<pair<int, int>> graph[10001];

vector<int> trace[501];

int N, M, S, D, U, V, P;

void MyDijstra()
{  
    for (int i = 0; i <= N; i++) disArr[i] = INF;

    for (int i = 0; i < M; i++) {
        cin >> U >> V >> P;
        graph[U].push_back(make_pair(V, P));
    }

    // 우선순위 큐에 삽입.
    mypq.push({ 0, S }); // < first : 거리 , second : 노드 인덱스 >

    disArr[S] = 0;

    while (!mypq.empty()) {
        // -를 붙이는 이유는 우선순위 큐를 이용하여 정렬하기 위함이다.
        // (최소힙으로 구현)
        int ncost = -mypq.top().first;
        int now = mypq.top().second;

        mypq.pop();

        // 이미 담겨 있는 것보다 거리가 크면 넘어간다.
        if (disArr[now] < ncost) continue;

        // 해당 노드에서 연결된 모든 경로를 확인
        for (int i = 0; i < graph[now].size(); i++) {
            // dissum = 임시 노드 + 현재 노드에서 i로가는 비용
            int dissum = ncost + graph[now][i].second;
            // 비용이 더 작다면 최단경로 테이블 값을 갱신.
            // 같아도 확인이 필요하다.
            // 최소 거리가 여러개 있을 수 있기 떄문
            if (dissum <= disArr[graph[now][i].first]) {

                if (dissum < disArr[graph[now][i].first]) {
                
                    // 임시 노드 업데이트
                    disArr[graph[now][i].first] = dissum;

                    trace[graph[now][i].first].clear(); // 새로 갱신한다면 전에 있던 것이 필요가 없다.
                    trace[graph[now][i].first].push_back(now); // 경로를 저장

                    // 우선순위 큐에 (거리, 노드 인덱스) 푸시
                    mypq.push(make_pair(-dissum, graph[now][i].first));
                }
                else trace[graph[now][i].first].push_back(now); // 경로를 저장 역방향으로 넣어준다.
            }
        }
    }

    // 최단 거리의 경로를 삭제해 줍니다.
    queue<int> delQ;
    delQ.push(D);
    while (!delQ.empty()) {
        int nowDel = delQ.front();
        delQ.pop();
        for (int i = 0; i < trace[nowDel].size(); i++) {
            for (auto it = graph[trace[nowDel][i]].begin(); it != graph[trace[nowDel][i]].end(); it++) {
                if ((*it).first == nowDel) {
                    delQ.push(trace[nowDel][i]);
                    graph[trace[nowDel][i]].erase(it);
                    break;
                }
            }
        }
    }


    // 새로운 데이크스트라를 진행하여 거의 최단 경로를 찾는다.
    for (int i = 0; i <= N; i++) disArr[i] = INF;
    // 우선순위 큐에 삽입.
    mypq.push({ 0, S }); // first : 거리 , second : 노드 인덱스
    disArr[S] = 0;
    while (!mypq.empty()) {
        // -를 붙이는 이유는 우선순위 큐를 이용하여 정렬하기 위함이다.
        // (최소힙으로 구현)
        int ncost = -mypq.top().first;
        int now = mypq.top().second;

        mypq.pop();

        // 이미 담겨 있는 것보다 거리가 크면 넘어간다.
        if (disArr[now] < ncost) continue;

        // 해당 노드에서 연결된 모든 경로를 확인
        for (int i = 0; i < graph[now].size(); i++) {
            // dissum = 임시 노드 + 현재 노드에서 i로가는 비용
            int dissum = ncost + graph[now][i].second;
            // 비용이 더 작다면 최단경로 테이블 값을 갱신.
            if (dissum < disArr[graph[now][i].first]) {

                disArr[graph[now][i].first] = dissum;
                // 우선순위 큐에 (거리, 노드 인덱스) 푸시
                mypq.push(make_pair(-dissum, graph[now][i].first));
            }
        }
    }

    for (int i = 0; i <= N; i++) trace[i].clear();
    for (int i = 0; i <= M; i++) graph[i].clear();
}


int main()
{
    ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
    //cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
    cin.tie(NULL);
    std::cout.tie(NULL);

    while (true) {

        cin >> N >> M;

        if (N == 0 && M == 0) break;

        cin >> S >> D;

        MyDijstra();

        if (disArr[D] == INF) cout << -1 << "\n";
        else cout << disArr[D] << "\n";
    }

    return 0;
}

틀린 코드를 포기할 수 없어 여러가지 방법으로 접근하여 메모리를 줄여보았지만 의미는 없었다.

백준 5719번 (거의 최단 경로, C++, Dijkstra) / 추가 반례 [BAEKJOON]

거의 최단 경로

문제

입력

출력

예제 출력 1

예제 입력 1

출처

알고리즘 분류

추가 예제

예제 출력 A

예제 출력 A

예제 입력 B

예제 출력 B

예제 입력 C

예제 출력 C

예제 입력 D

예제 출력 D

틀린 코드 (메모리 초과)

통과된 코드

댓글 달기 댓글 취소

거의 최단 경로

문제

입력

출력

예제 출력 1

예제 입력 1

출처

알고리즘 분류

추가 예제

예제 출력 A

예제 출력 A

예제 입력 B

예제 출력 B

예제 입력 C

예제 출력 C

예제 입력 D

예제 출력 D

틀린 코드 (메모리 초과)

통과된 코드

댓글 달기 댓글 취소

관련 게시물