숫자 카드
https://www.acmicpc.net/problem/10815
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 256 MB | 70735 | 32252 | 23137 | 44.720% |
문제
숫자 카드는 정수 하나가 적혀져 있는 카드이다.
상근이는 숫자 카드 N개를 가지고 있다.
정수 M개가 주어졌을 때,
이 수가 적혀있는 숫자 카드를 상근이가 가지고 있는지 아닌지를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다.
둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다.
숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다.
두 숫자 카드에 같은 수가 적혀있는 경우는 없다.
셋째 줄에는 M(1 ≤ M ≤ 500,000)이 주어진다.
넷째 줄에는 상근이가 가지고 있는 숫자 카드인지 아닌지를 구해야 할 M개의 정수가 주어지며,
이 수는 공백으로 구분되어져 있다. 이 수도 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다
출력
첫째 줄에 입력으로 주어진 M개의 수에 대해서,
각 수가 적힌 숫자 카드를 상근이가 가지고 있으면 1을, 아니면 0을 공백으로 구분해 출력한다.
예제 입력 1
5 6 3 2 10 -10 8 10 9 -5 2 3 4 5 -10
예제 출력 1
1 0 0 1 1 0 0 1
출처
알고리즘 분류
순회 형식으로 구현하면 숫자 하나를 확인할때 마다 500,000번의 연산이 필요하다. (시간 초과)
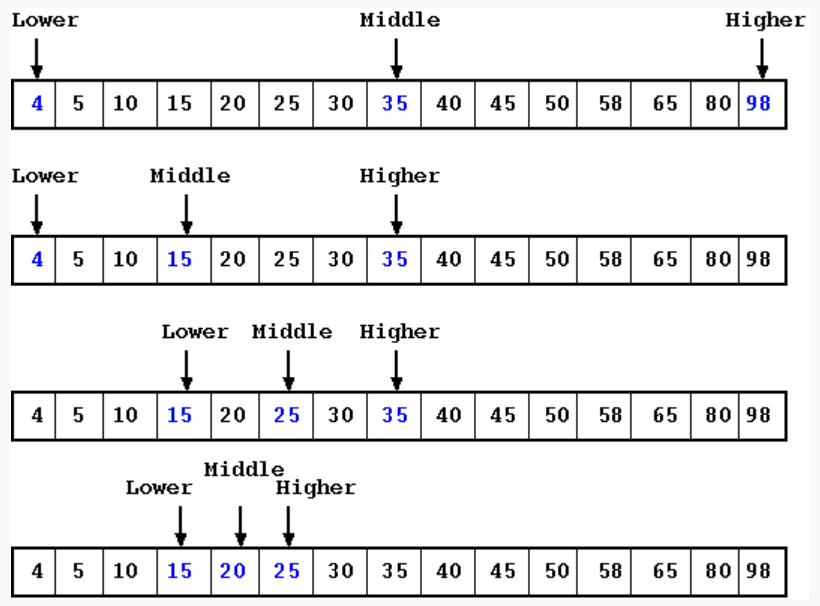
순회로 확인하는 방법보다 더 빠른 탐색 방법이 필요한데
이럴 때 binary search를 이용하여 탐색의 시간 복잡도를 O(logN)으로 만들 수 있다.
코드는 재귀적으로 작성하였고 해설 참고하면 쉽게 이해가 가능하다.
통과된 코드
#include <iostream>
#include <algorithm>
using namespace std;
constexpr int MAX = 500000;
int arr[MAX];
int N , M, target;
// 이분 탐색 함수
bool BinarySearch(int tArr[MAX], int start, int end, int target)
{
if (start > end) return false; // 만족하는 결과가 없다 false return
int mid = (start + end) / 2; // 중간 값을 찾아준다.
if (arr[mid] == target) return true; // 만족하는 결과!! true return
// 찾는 수가 더 작다면, 검사 범위를 더 작게해서 다시 이분탐색 // 결과가 나오면 return
// 찾는 수가 더 크면, 검사 범위를 더 크게해서 다시 이분탐색 // 결과가 나오면 return
if (arr[mid] > target) return BinarySearch(arr, start, mid - 1, target);
else return BinarySearch(arr, mid + 1, end, target);
}
int main()
{
ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
cin.tie(NULL);
cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++) cin >> arr[i];
// 이분 탐색을 위한 오름차순 정렬을 수행한다.
sort(arr, arr + N);
// 탐색할 숫자의 개수를 입력받는다.
cin >> M;
for (int i = 0; i < M; i++) {
cin >> target;
// 이진 탐색 후 출력
cout << BinarySearch(arr, 0, N - 1, target) << "\n";
}
return 0;
}


![백준 2562번 (최댓값, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/2022/10/boj-og-1-2048x1070-1-1024x535.png)
![백준 6568번 (귀도 반 로썸은 크리스마스날 심심하다고 파이썬을 만들었다, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)
![Programmers 17684 [3차] 압축 [2018 KAKAO BLIND RECRUITMENT]](https://lycos7560.com/wp-content/uploads/2023/03/programmers.jpg)