쉬운 계단 수
https://www.acmicpc.net/problem/10844
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 256 MB | 116877 | 36976 | 26702 | 29.843% |
문제
45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다.
이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자.
0으로 시작하는 수는 계단수가 아니다.
입력
첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
예제 입력 1
1
예제 출력 1
9
예제 입력 2
2
예제 출력 2
17
예제 입력 A
100
예제 출력 A
18404112
예제 입력 B
70
예제 출력 B
564706557
출처
- 문제를 만든 사람: baekjoon
알고리즘 분류
접근하는 방법
N = 1 => 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 (0으로 시작하는 수는 계단수가 아니다.)
N = 2 => 10 / 12 / 21 / 23 / 32 / 34 / 43 / 45 / 54 / 56 / 65 / 67 / 76 / 78 / 87 / 89 / 98
N = 3 => 101 / 121 / 123 / 210 / 212 / 321 / 324 ….
N = 2 일 경우를 예시로 들어보면
마지막 숫자 전 수가 2인 경우 마지막 숫자에 올 수 있는 수는 1, 3 – 2가지의 경우 / 21, 23
마지막 숫자 전 수가 3인 경우 마지막 숫자에 올 수 있는 수는 2, 4 – 2가지의 경우 / 32, 34
마지막 숫자가 0 이라면 1가지의 경우 / 10
마지막 숫자가 9 라면 1가지의 경우 / 89
위의 내용을 표로 정리하면 아래와 같이 나온다.
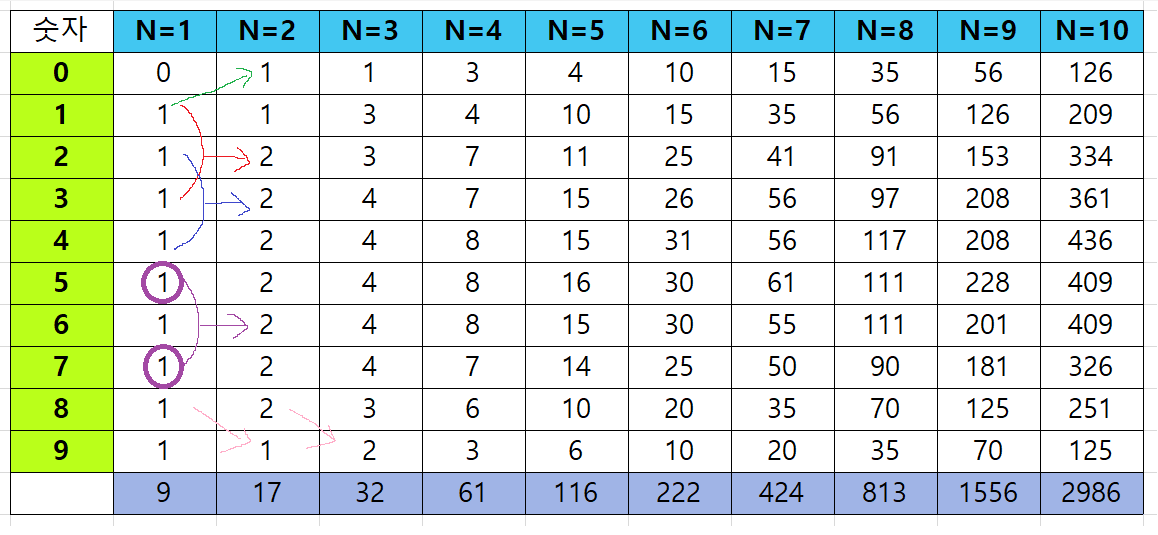
N의 범위는 1<= N <= 100
구하는 값은 계단 수의 개수를 1,000,000,000으로 나눈 나머지를 출력하는 것
통과된 코드
#include <iostream>
using namespace std;
constexpr int MOD = 1000000000;
int N;
// dp[i][j]
// i = 숫자, j = 자릿수
long long dp[10][101];
// DP 초기화
void DP_Initialization()
{
dp[0][1] = 0;
for (int i = 1; i < 10; i++) {
dp[i][1] = 1;
}
}
int main()
{
cin >> N;
long long result = 0;
DP_Initialization();
for (int j = 2; j <= N; j++) {
for (int i = 0; i < 10; i++) {
if (i == 0) { // 마지막 숫자가 0
dp[i][j] = dp[1][j-1];
}
else if (i == 9) { // 마지막 숫자가 9
dp[i][j] = dp[8][j-1];
}
else {
// 모듈러 연산 덧셈
dp[i][j] = ( (dp[i-1][j-1] % MOD) + ( dp[i + 1][j - 1] % MOD) ) % MOD;
}
}
}
for (int i = 0; i < 10; i++) {
result += ( dp[i][N] % MOD ); // 모듈러 연산 덧셈
}
cout << result % MOD; // 모듈러 연산 덧셈
return 0;
}

DP 문제는 점화식을 만들기가 너무 어려운 것 같다.
문제가 이해하기 어렵다면 아래의 영상을 시청하는 것을 추천


![백준 10824번 (네 수, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)