백양로 브레이크
https://www.acmicpc.net/problem/11562
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 256 MB | 2698 | 1354 | 1024 | 47.828% |
문제
서울 소재 Y모 대학교에서 대규모 공사를 진행하면서, 학교가 마치 미로처럼 변해버리고 말았다.
공사 이전까지는 어떤 건물에서 출발하더라도 다른 모든 건물로 갈 수 있는 길이 있었으나,
공사가 진행되면서 어떻게 한 건진 알 수 없지만 일방통행만 가능한 길이 많이 늘고 말았다.
컴퓨터과학과 학생 남규는 전공 수업을 듣고 교양 수업을 들으러 가던 중
길을 잃어 3일 밤낮을 헤매다가 공학관에서 종합관으로 가는 길은 존재하지 않는다는 결론을 내렸다.
3일 사이에 과제도 내지 못하고 출석도 하지 못해 학사경고 위기에 처한 남규는 전공을 살려
현재 일방통행인 길들 중 반드시 양방향으로 바꿔야만 하는 길이 몇 개인지 조사해 학교에 건의하기로 마음을 먹었다.
남규는 여러 건물들 사이를 직접 잇는 길들을 모두 조사했고,
그 중 어떤 길들이 일방통행인지, 또는 양방향 통행이 가능한지를 모두 체크했다.
남규의 프로그램은 간단하다.
출발지와 도착지를 입력하면 도착지까지 가기 위해 최소 몇 개의 길을 양방향으로 바꿔야만 하는지를 출력해준다.
프로그램이 완성되었다는 소문이 퍼지자, 남규처럼 길을 잃고 헤맨 경험이 있는 학생들은 남규에게 묻기 시작했다.
“공학관에서 대강당 갈 수 있어?”
“상경대 별관에서 학관으로는?”
남규는 매번 손으로 타이핑해 입력하고 결과를 보내주는 데에 지치고 말았다.
결국 앓아누운 남규를 위해 학생들의 질문을 해결할 새로운 프로그램을 만들어보자.
입력
첫 줄에 Y대학교 건물의 수 n과 길의 수 m이 주어진다. (n ≤ 250, m ≤ n * (n – 1) / 2 )
다음 m줄에 걸쳐, u v b (1 ≤ u ≤ n, 1 ≤ v ≤ n, u != v, b = 0 또는 1) 의 형태로 길에 대한 정보가 주어진다.
b가 0일 경우 u에서 v로 가는 일방통행 길인 것이고, b가 1일 경우 u와 v를 잇는 양방향 길이다.
어떤 두 건물 사이를 잇는 길은 최대 한 개이다.
다음 줄에 학생들의 질문의 수 k가 주어진다. (1 ≤ k ≤ 30,000)
다음 k줄에 걸쳐 s e (1 ≤ s ≤ n, 1 ≤ e ≤ n)의 형태로 학생들의 질문들이 주어진다.
이는 질문한 학생이 건물 s에서 건물 e로 가고 싶다는 의미이다.
출력
출력은 k줄에 걸쳐 이루어진다.
각 질문에 대해, 최소 몇 개의 일방통행인 길을 양방향 통행으로 바꿔야 출발지에서 도착지로 갈 수 있는지를 출력한다.
모든 길을 양방향으로 바꾸더라도 서로 도달 불가능한 건물은 없다.
예제 입력 1
4 3 1 2 0 2 3 1 3 4 0 7 1 1 1 2 2 1 1 4 4 1 2 3 4 3
예제 출력 1
0 0 1 0 2 0 1
출처
University > 연세대학교 > 2015 연세대학교 프로그래밍 경시대회 F번
- 문제를 만든 사람: portableangel
알고리즘 분류
접근 방법
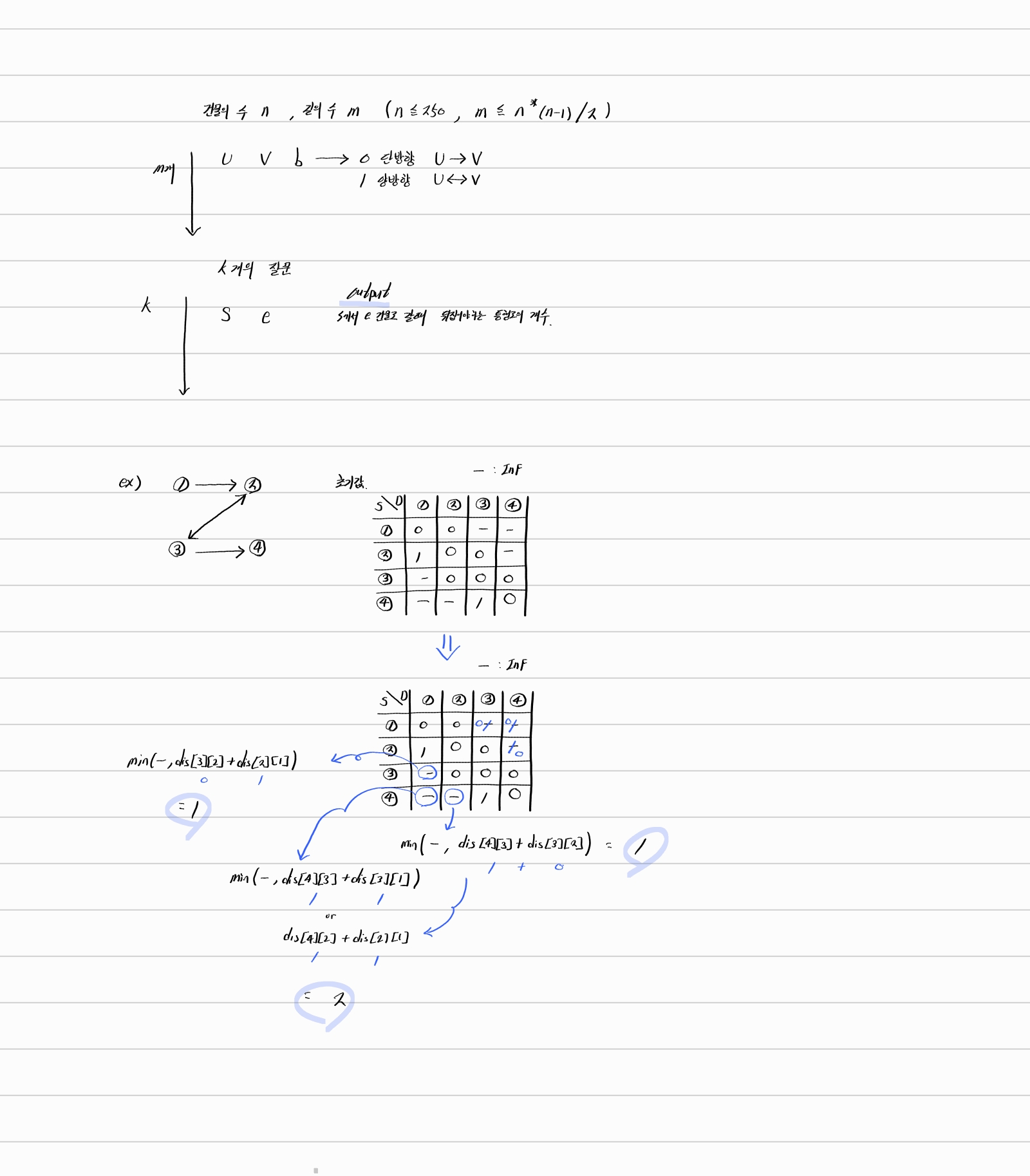
시간 초과 코드 (DFS)
DFS 탐색을 이용하여 도착지부터 출발지까지 최소 거리를 카운트하여 탐색한 코드
#include <iostream>
#include <vector>
#include <list>
using namespace std;
constexpr int INF = INT32_MAX / 2;
constexpr int MAX = 251;
vector<pair<int, int>> graph[MAX];
list<pair<int, int>> myList;
int disArr[MAX][MAX];
bool check[MAX];
// N : 도시의 수, M : 길의 수
int N, M, s, d, w, b, K, result;
void Tracking(int start, int now, int cnt)
{
if (start == now || disArr[now][start] == 0) {
result = min(result, cnt);
return;
}
for (int j = 0; j < graph[now].size(); j++) {
int v = graph[now][j].first; // 도착점
int weight = graph[now][j].second; // 가중치
if (check[v] == true) continue;
if (weight == INF) {
cnt++;
check[v] = true;
Tracking(start, v, cnt);
check[v] = false;
cnt--;
}
else
{
check[v] = true;
Tracking(start, v, cnt);
check[v] = false;
}
}
}
int main()
{
ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
cin.tie(NULL);
cout.tie(NULL);
cin >> N >> M;
// 길의 정보를 입력
for (int i = 0; i < M; i++) {
// 출발 s, 도착 d, b 양/단 방향
cin >> s >> d >> b;
if (b == 0) { // 단방향
graph[s].push_back(make_pair(d, 0));
graph[d].push_back(make_pair(s, INF));
}
else { // 양방향
graph[s].push_back(make_pair(d, 0));
graph[d].push_back(make_pair(s, 0));
}
}
// 질문을 입력 받는다.
cin >> K;
pair<int, int> tempP;
while (K--) {
cin >> tempP.first >> tempP.second;
myList.push_back(tempP);
}
// 최단 거리 배열 disArr 배열을 INF 초기화
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (i == j) disArr[i][j] = 0;
else disArr[i][j] = INF;
}
}
for (int i = 1; i <= N; i++) { // 시작 정점
for (int j = 0; j < graph[i].size(); j++) {
int v = graph[i][j].first; // 도착점
int weight = graph[i][j].second; // 가중치
if (disArr[i][v] > weight) disArr[i][v] = weight;
}
}
// 무지성 플로이드
for (int k = 1; k <= N; k++) {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (i == j) disArr[i][j] = 0;
else disArr[i][j] = min(disArr[i][j], disArr[i][k] + disArr[k][j]);
}
}
}
for (auto it = myList.begin(); it != myList.end(); it++) {
result = INF;
if (disArr[it->first][it->second] == 0) cout << disArr[it->first][it->second] << "\n";
else {
Tracking(it->second, it->first, 0);
cout << result << "\n";
}
}
return 0;
}
통과된 코드
Floyd-Warshall 알고리즘이 어떤 식으로 작동하는지 안다면 뒤집는 부분에 왜 1 이 들어가는지 알 수 있다.
#include <iostream>
#include <vector>
#include <list>
using namespace std;
constexpr int INF = INT32_MAX / 2;
constexpr int MAX = 251;
vector<pair<int, int>> graph[MAX];
list<pair<int, int>> myList;
int disArr[MAX][MAX];
// N : 도시의 수, M : 길의 수
int N, M, s, d, w, b, K, result;
int main()
{
ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
cin.tie(NULL);
cout.tie(NULL);
cin >> N >> M;
// 최단 거리 배열 disArr 배열을 INF 초기화
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
disArr[i][j] = INF;
}
}
// 길의 정보를 입력
for (int i = 0; i < M; i++) {
// 출발 s, 도착 d, b 양/단 방향
cin >> s >> d >> b;
if (b == 0) { // 단방향
graph[s].push_back(make_pair(d, 0));
disArr[d][s] = 1; // (disArr[i][k] + disArr[k][j] vs INF)
}
else { // 양방향
graph[s].push_back(make_pair(d, 0));
graph[d].push_back(make_pair(s, 0));
}
}
// 질문을 입력 받는다.
cin >> K;
pair<int, int> tempP;
while (K--) {
cin >> tempP.first >> tempP.second;
myList.push_back(tempP);
}
for (int i = 1; i <= N; i++) { // 시작 정점
for (int j = 0; j < graph[i].size(); j++) {
int v = graph[i][j].first; // 도착점
int weight = graph[i][j].second; // 가중치
if (disArr[i][v] > weight) disArr[i][v] = weight;
}
}
// 무지성 플로이드
for (int k = 1; k <= N; k++) {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (i == j) disArr[i][j] = 0;
else disArr[i][j] = min(disArr[i][j], disArr[i][k] + disArr[k][j]);
}
}
}
for (auto it = myList.begin(); it != myList.end(); it++) {
cout << disArr[it->first][it->second] << "\n";
}
return 0;
}


![백준 3190번 (뱀, C++, Queue, Simulation ) / 추가 반례 [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)
![백준 1182번 (부분수열의 합, C++, DFS) / 추가 반례 [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og-1.png)