비숍
https://www.acmicpc.net/problem/1799
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 10 초 | 128 MB | 22527 | 5606 | 3885 | 24.324% |
문제
서양 장기인 체스에는 대각선 방향으로 움직일 수 있는 비숍(bishop)이 있다.
< 그림 1 >과 같은 정사각형 체스판 위에 B라고 표시된 곳에 비숍이 있을 때
비숍은 대각선 방향으로 움직여 O로 표시된 칸에 있는 다른 말을 잡을 수 있다.
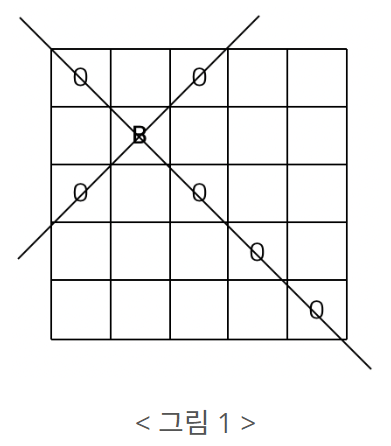
그런데 체스판 위에는 비숍이 놓일 수 없는 곳이 있다.
< 그림 2 >에서 체스판에 색칠된 부분은 비숍이 놓일 수 없다고 하자.
이와 같은 체스판에 서로가 서로를 잡을 수 없도록 하면서 비숍을 놓는다면 < 그림 3 >과 같이 최대 7개의 비숍을 놓을 수 있다.
색칠된 부분에는 비숍이 놓일 수 없지만 지나갈 수는 있다.

정사각형 체스판의 한 변에 놓인 칸의 개수를 체스판의 크기라고 한다.
체스판의 크기와 체스판 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 주어질 때,
서로가 서로를 잡을 수 없는 위치에 놓을 수 있는 비숍의 최대 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 체스판의 크기가 주어진다.
체스판의 크기는 10이하의 자연수이다.
둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로 한 줄씩 주어진다.
비숍을 놓을 수 있는 곳에는 1, 비숍을 놓을 수 없는 곳에는 0이 빈칸을 사이에 두고 주어진다.
출력
첫째 줄에 주어진 체스판 위에 놓을 수 있는 비숍의 최대 개수를 출력한다.
예제 입력 1
5 1 1 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 0 0 1 0 1 1 1
예제 출력 1
7
출처
Olympiad > 한국정보올림피아드 > 한국정보올림피아드시․도지역본선 > 지역본선 2007 > 초등부 5번
알고리즘 분류
비숍은 같은 색깔의 비숍만 잡을 수 있다.
다른 색에 있는 비숍까지 모든 경우의 수를 고려한다면 시간 초과가 발생
아래의 코드는 재귀적으로 BackTracking을 구현한 코드
N x N 크기의 체스판에서 N개의 퀸을 배치하는 모든 경우를 탐색
각 칸마다 O(N) 시간이 소요되고, N x N 크기의 체스판에 N개의 퀸을 배치하므로
총 시간 복잡도는 O(N^N) => 시간초과
시간 초과 코드
#include <iostream>
using namespace std;
constexpr int _MAX = 10;
int _N, _Res;
bool _Map[_MAX][_MAX];
bool _Dx[19], _Dy[19];
void BackTracking(int _Cnt, int _x)
{
int _dxy, _sum;
for (int i = _x; i < _N; i++)
for (int j = 0; j < _N; j++) {
if (!_Map[i][j]) continue;
_dxy = i - j + _N - 1;
_sum = i + j;
if (_Dx[_dxy] || _Dy[i + j]) continue;
_Dx[_dxy] = true;
_Dy[_sum] = true;
BackTracking(_Cnt + 1, i);
_Dx[_dxy] = false;
_Dy[_sum] = false;
}
_Res = max(_Res, _Cnt);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> _N;
for (int i = 0; i < _N; i++)
for (int j = 0; j < _N; j++)
cin >> _Map[i][j];
BackTracking(0, 0);
cout << _Res;
return 0;
}

통과된 코드
아래의 코드는 하얀 칸에 올 수 있는 비숍의 최댓값과
검은칸에 올 수 있는 비숍의 최댓값을 따로 구한 후 합한 결과를 출력해준다.
비숍을 해당 칸에 놓는 경우 / 안 놓는 경우 => 2가지
N / 2 칸을 N^2으로 탐색하지만 흑/백 2번이므로 => N^2
약 O(2^N^2)의 시간 복잡도를 가진다.
#include <iostream>
using namespace std;
constexpr int _MAX = 10;
int _N, _Res, _ResSum;
bool _Map[_MAX][_MAX];
bool _CheckX[19], _CheckY[19];
void CheckBishop(int _bishopCnt, int _x, bool _isOdd)
{
int _dxy, _sum;
for (int i = _x; i < _N; i++)
for (int j = 0; j < _N; j++) {
if (!_Map[i][j]) continue;
_dxy = i - j + _N - 1;
_sum = i + j;
if (_CheckX[_dxy] || _CheckY[i + j] || _sum % 2 == _isOdd) continue;
_CheckX[_dxy] = true;
_CheckY[_sum] = true;
CheckBishop(_bishopCnt + 1, i, _isOdd);
_CheckX[_dxy] = false;
_CheckY[_sum] = false;
}
_Res = max(_Res, _bishopCnt);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> _N;
for (int i = 0; i < _N; i++)
for (int j = 0; j < _N; j++)
cin >> _Map[i][j];
CheckBishop(0, 0, false);
_ResSum += _Res;
_Res = 0;
CheckBishop(0, 0, true);
_ResSum += _Res;
cout << _ResSum;
return 0;
}

제출된 답 중에서 0ms 도 있다… 세상에는 괴물이 많다.

![백준 1806번 (부분합, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)
![백준 12891번 (DNA 비밀번호, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og-1.png)
A former soldier leaves society to turn out to be a mountain man in this 1972 movie.