평범한 배낭

https://www.acmicpc.net/problem/12865

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
2 초	512 MB	85465	31511	20447	35.292%

문제

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다.

세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다.

각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다.

아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다.

준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다.

두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.

입력으로 주어지는 모든 수는 정수이다.

출력

한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

예제 입력 1

4 7
6 13
4 8
3 6
5 12

예제 출력 1

14

출처

• 문제를 만든 사람: Acka
• 데이터를 추가한 사람: leedongbin, skyoliver

알고리즘 분류

• 다이나믹 프로그래밍
• 배낭 문제

---

문제 정리

N개의 물건 (1 ≤ N ≤ 100)

물건은 무게 W와 가치 V를 가지고 있다. (1 ≤ W ≤ 100,000 / 0 ≤ V ≤ 1,000)

K만큼의 무게만을 넣을 수 있는 배낭 (1 ≤ K ≤ 100,000)

원하는 답은 배낭에 넣을 수 있는 물건들의 가치의 최댓값

첫 줄 => 물품의 수 N 과 버틸 수 있는 무게 K

N 줄 => 물건의 무게 W / 물건의 가치 V

잘못된 접근법

만약 물건이 2개라고 가정한다면 (A, B)

A를 가방에 넣고 / 안넣고 2가지의 경우의 수 (2)

B를 가방에 넣고 / 안넣고 2가지의 경우의 수 (2)

=> 총 2^2의 경우의 수가 발생한다. (2) x (2)

물건의 수가 적을 경우에는 각 경우에서 가방에 넣은 물건들의 무게와 가치 등을 이용하여

문제를 해결할 수 있지만 물건의 개수는 총 100개 까지 가능하므로

100개 2^100의 경우의 수가 나온다.

2^100은 1,267,650,600,228,229,401,496,703,205,376

1,267,650,600,228,229,401,496,703,205,376의 경우에 수를 모두 확인 한다면 당연하게 시간 초과로 고통을 받을 것이다.

그러므로 위와 같은 접근은 잘못된 접근 방법이다.

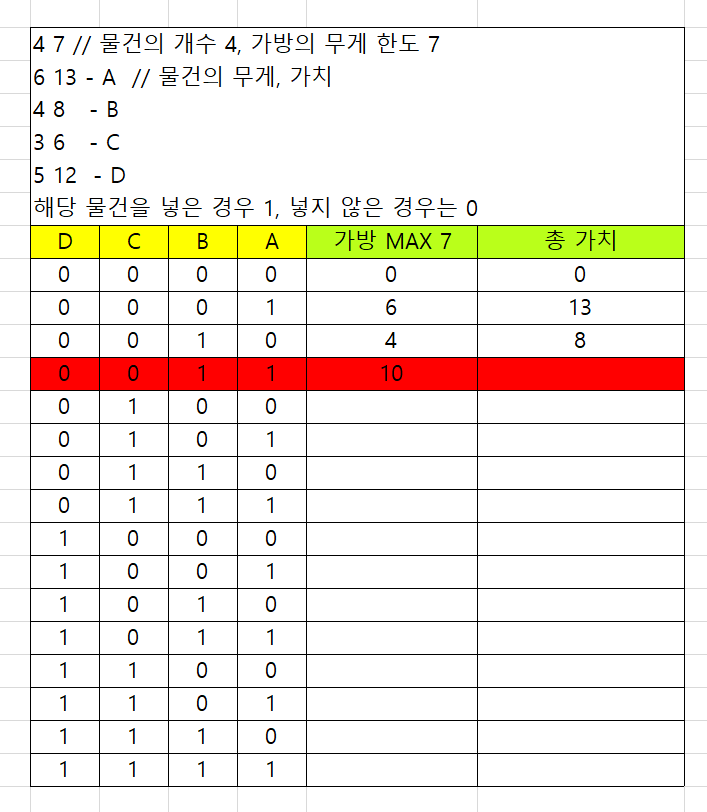
0011 즉 A,B가 같이 가방에 들어간다면 가방의 하중을 넘어서 답이 될 수 없다.

0011이 답이 될 수 없다면 결국 1011, 1100, 0100 도 답에서 제외가 된다.

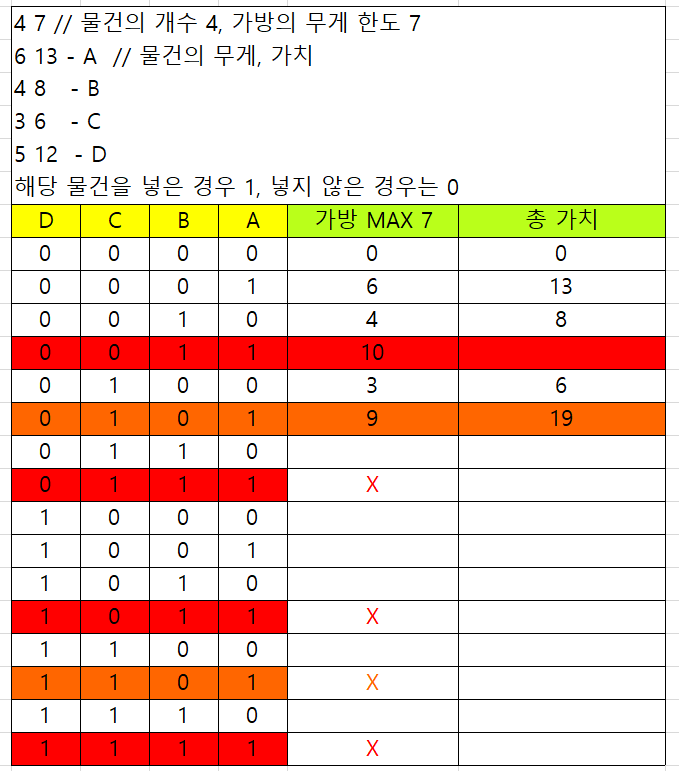
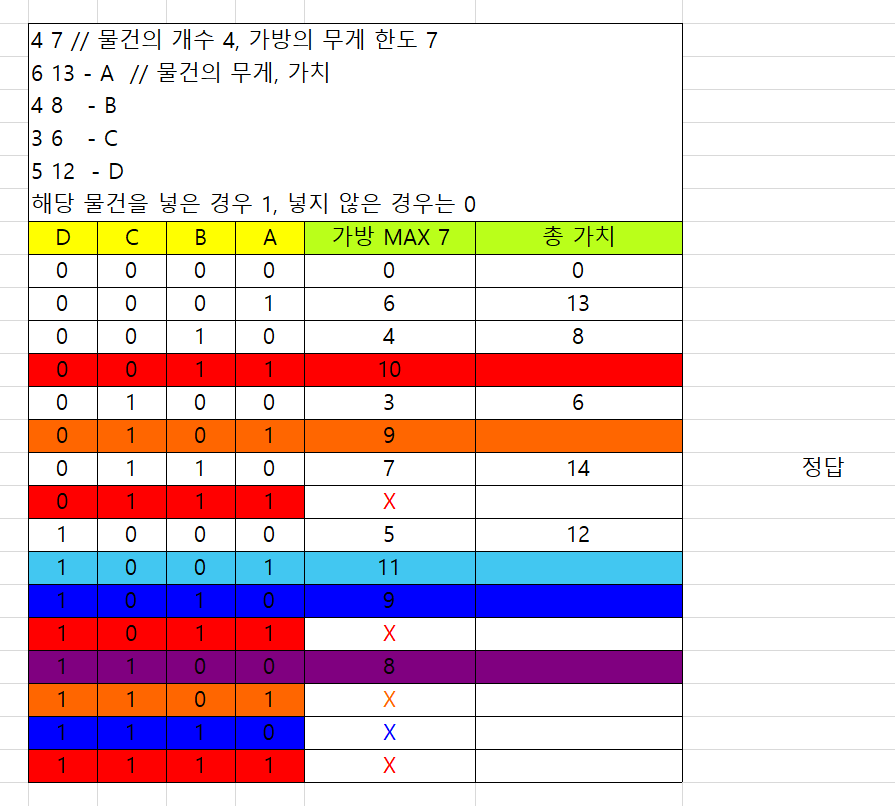
진행하면서 많은 경우의 수를 줄일 수 있지만 코딩하기도 쉽지 않고 배열을 선언하는 것도 난감하다.

다른 방향으로 접근이 필요하다.

---

가방의 무게를 기준으로 접근

통과된 코드

#include <iostream>

using namespace std;

// 물건의 개수 N와 가방의 무게 한도 K
int N, K;

// 아이템의 무게를 저장, 아이템의 가치를 저장
int iW[101], iV[101];

// [i][j] 
// i => 물건의 순서 / j => 가방의 무게
int arr[101][100001];

void GetInput()
{
	// 물건의 개수와 가방의 무게 한도 입력 받기
	cin >> N >> K;

	int cnt = 1;
	while (cnt <= N) { // 물건의 무게와 가치를 입력받음
		cin >> iW[cnt] >> iV[cnt];
		cnt++;
	}
}

int main()
{
	GetInput();

    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= K; j++) {
			if (j - iW[i] >= 0) {  // 가방 한도 - 현재 물건의 무게 
				// 물건을 넣을 수 있는 경우 (위의 연산이 >= 0)
				
				arr[i][j] = max(arr[i - 1][j], arr[i - 1][j - iW[i]] + iV[i]);
				// 둘중에서 최대 값을 찾는 함수 max
			}
			else { 
				// 물건을 넣을 수 없는 경우 (위의 연산이 음수)
				arr[i][j] = arr[i - 1][j];
			}
        }
    }

	// 마지막까지 연산한다면 arr[N][K] 값이 최대 가치가 된다.
	cout << arr[N][K];

	return 0;
}

DP 문제는 풀어도 풀어도 적응이 안된다.

이 문제만 3시간 정도 생각해봤는데 혼자서 해결 불가능… ㅠ

영상 및 블로그를 참고하면서 직접 손으로 해보면 어느 정도 감이 잡히는 것 같다.

도움된 자료

https://yabmoons.tistory.com/571 <- 블로그

https://gamedoridori.tistory.com/20 <- 블로그