벨만-포드 (Bellman–Ford Algorithm) 알고리즘
Bellman-Ford 알고리즘은 (Richard Bellman과 Lester Ford의 이름)
가중 그래프에서 정점과 다른 모든 정점 사이의 최단 경로를 찾는 데 사용되는 최단 경로 알고리즘입니다.
간단하게 말하면 한 정점에서 다른 정점까지의 최단 거리를 구하는 알고리즘입니다.
작동하는 과정
https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/
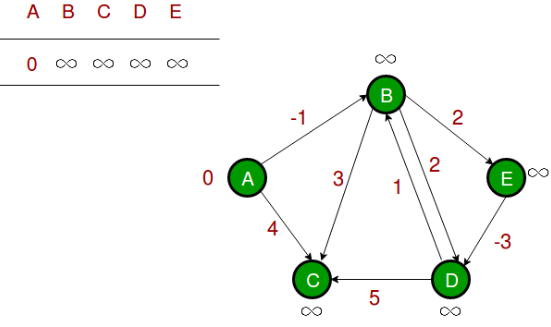
1단계: 출발 정점을 0으로 둡니다.
출발 정점의 거리를 제외하고 모든 거리를 무한으로 초기화합니다.
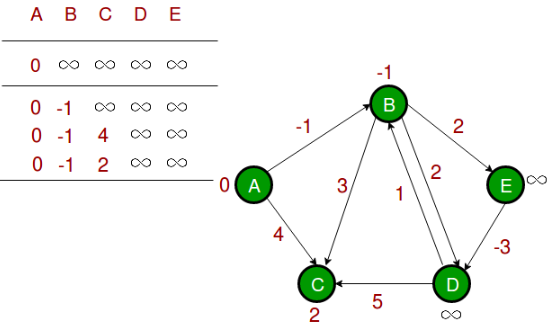
2단계: 모든 정점을 다음 순서로 처리합니다
(B, E), (D, B), (B, D), (A, B), (A, C), (D, C), (B, C), (E, D)
모든 모서리가 처음으로 처리될 때 다음과 같은 거리를 얻습니다.
첫 번째 행은 초기의 거리를 보여줍니다.
두 번째 행은 가장자리 (B, E), (D, B), (B, D) 및 (A, B)가 처리될 때 거리를 보여줍니다.
세 번째 행은 (A, C)가 처리될 때의 거리를 보여줍니다.
네 번째 행은 (D, C), (B, C) 및 (E, D) 를 처리한 거리를 보여줍니다.
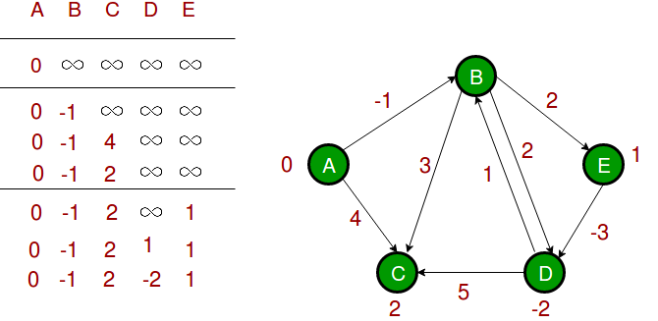
3단계: 첫 번째 반복은 최대 1 정점 길이의 모든 최단 경로를 제공합니다.
모든 정점이 두 번째로 처리 될 때 다음과 같은 거리를 얻습니다 (마지막 행은 최종 값을 나타냅니다).
4단계: 두 번째 반복은 최대 2 개의 가장자리 길이인 모든 최단 경로를 제공합니다.
알고리즘은 모든 정점을 2번 더 처리합니다.
두 번째 반복 후에는 거리가 최소화되므로
세 번째 및 네 번째 반복에서는 거리가 업데이트되지 않습니다.
주의 사항
Bellman-Ford 알고리즘을 사용할 경우 아래와 같은 음의 가중치 주기를 주의해야 합니다.

위의 예제는 1 -> 2 -> 3 순서를 계속 반복하면 가중치가 계속 줄어듭니다. (잘못된 결과)
위와 같은 상황에서는 Bellman-Ford 알고리즘으로 답을 구할 수 없습니다.
그래프에 음의 가중치 주기가 포함되어 있는지 확인하려면
Bellman-Ford 알고리즘 이후에 모든 간선을 다시 한번 확인합니다.
만약 업데이트가 일어난다면 음의 가중치가 포함되어있다는 의미 입니다.
구현 코드
백준 11657번 ‘타임머신’ 문제를 Bellman-Ford 알고리즘 코드 해결
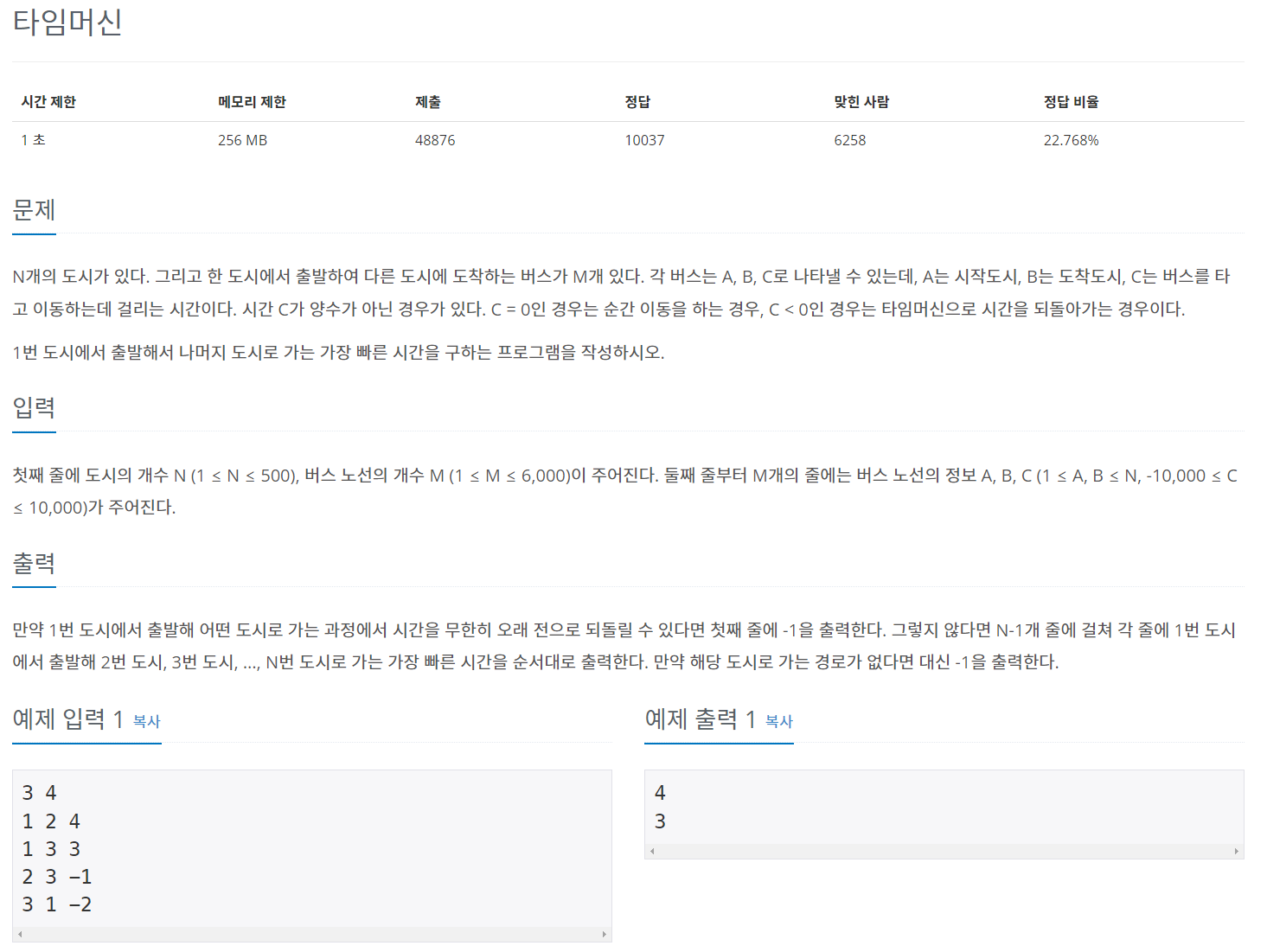
코드 C++
#include <iostream>
#include <vector>
using namespace std;
constexpr long long int INF = INT64_MAX;
constexpr int MAXN = 501;
long long int disArr[MAXN];
bool check = false; // 음의 순환이 있는지 확인
// N : 도시의 개수, M : 버스 노선의 개수
// A : 시작 도시, B : 도착 도시, C : 걸리는 시간
int N, M, A, B, C;
vector<pair<int, int>> graph[MAXN];
int main()
{
ios_base::sync_with_stdio(false); // scanf와 동기화를 비활성화
// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
cin.tie(NULL);
std::cout.tie(NULL);
cin >> N >> M;
for (int i = 0; i < M; i++) {
cin >> A >> B >> C;
// 단방향
graph[A].push_back(make_pair(B, C));
}
// 배열 초기화
fill(disArr, disArr + MAXN, INF);
disArr[1] = 0;
for (int k = 1; k <= N; k++) {// (모든 정점의 수 - 1) 번 확인한다.
// 모든 노선을 확인한다.
for (int i = 1; i <= N; i++) {
for (int j = 0; j < graph[i].size(); j++) {
int u = i; // 시작점
int v = graph[i][j].first; // 도착점
int weight = graph[i][j].second; // 가중치
// 만약 임시 배열이 무한대가 아니고 &&
// 시작 임시 배열의 가중치가 도착지의 가중치보다 작다면
if (disArr[u] != INF && disArr[u] + weight < disArr[v]) {
disArr[v] = disArr[u] + weight; // 임시배열을 업데이트 해준다.
// K가 N-1일때 모든 정점을 확인한 후
// K가 N일때 업데이트가 있다면 음의 순환이 있다는 이야기
if (k == N) {
cout << "-1";
return 0;
}
}
}
}
}
for (int i = 2; i <= N; i++) {
if (disArr[i] == INF) cout << "-1" << "\n";
else cout << disArr[i] << "\n";
}
return 0;
}
Dijkstra 알고리즘 vs Bellman–Ford 알고리즘
1. 가중치의 차이
예전에 정리한 Dijkstra 도 Bellman–Ford 와 같은 최단 경로 알고리즘입니다.
하지만 Dijkstra 알고리즘은 가중치가 양수일 때만 사용 가능하다는 중요한 특징을 가지고 있습니다.
따라서 가중치가 전부 양수라면 Dijkstra 알고리즘을 사용하고
하나라도 음수의 가중치가 있다면
Bellman–Ford 알고리즘을 사용해야 합니다.
위 : Dijkstra / 아래 Bellman–Ford (.gif)
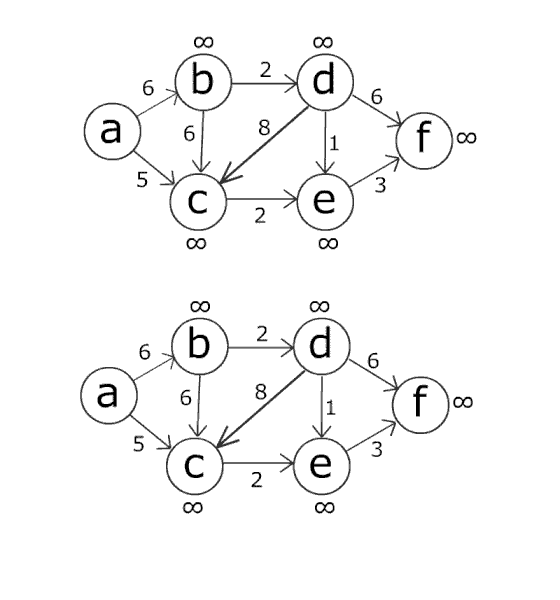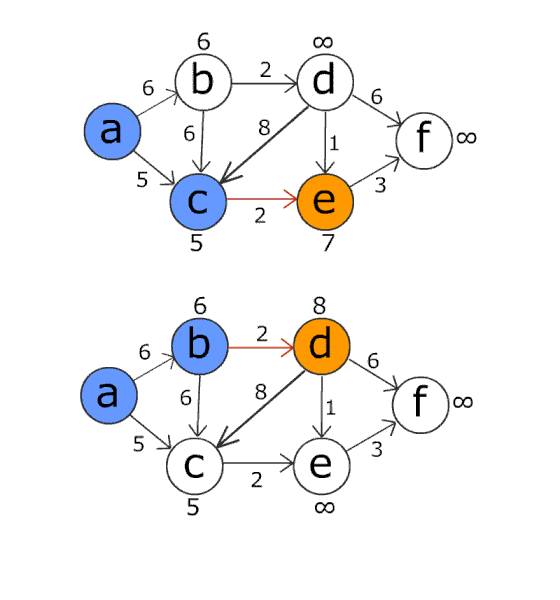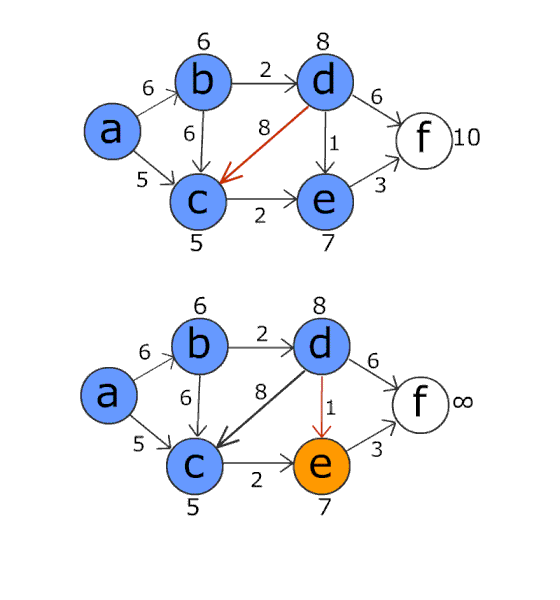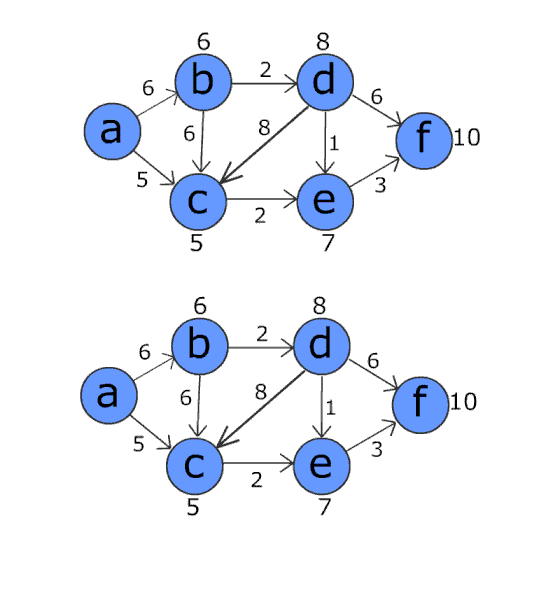
2. 시간 복잡도의 차이
V는 꼭짓점의 수이고 E는 간선의 개수라고 한다면
Dijkstra 알고리즘은 O(E*logV)의 시간 복잡도를 가지고
Bellman-Ford 알고리즘은 O(V*E)의 시간 복잡도를 가집니다.
따라서 음의 가중치가 없다면 Bellman-Ford 알고리즘보다는
Dijkstra 알고리즘을 이용하여 해결하는 것이 더 좋은 방법입니다.
(Dijkstra 알고리즘은 우선순위 대기열을 사용하여 처리해야 하는 정점을 유지하는 반면,
Bellman-Ford 알고리즘은 가장 짧은 경로를 찾기 위해 모든 정점에 대해 반복합니다.)
백준 11657번 (타임머신, C++, Bellman–Ford) [BAEKJOON]
백준 1738번 (골목길, C++, Bellman–Ford) / 추가 반례 [BAEKJOON]
알고리즘 – 벨만-포드 (Bellman–Ford Algorithm) 알고리즘 정리
백준 1219번 (오민식의 고민, C++, Bellman–Ford) [BAEKJOON]
백준 1865번 (웜홀, C++, Bellman–Ford) [BAEKJOON]
https://www.acmicpc.net/problemset?sort=ac_desc&algo=10 <- 백준 Bellman-Ford 알고리즘 문제