Dynamic Programming [DP] (다이나믹 프로그래밍 / 동적 계획법)
https://ko.wikipedia.org/wiki/%EB%8F%99%EC%A0%81_%EA%B3%84%ED%9A%8D%EB%B2%95
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법
부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다.
주어진 문제를 풀기 위해서, 문제를 여러 개의 하위 문제(subproblem)로 나누어 푼 다음,
그것을 결합하여 최종적인 목적에 도달하는 것이다.
각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 그것을 간단하게 해결할 수 있다.
이러한 방법으로 동적 계획법은 계산 횟수를 줄일 수 있다.
특히 이 방법은 하위 문제의 수가 기하급수적으로 증가할 때 유용하다.
“하나의 문제를 단 한번만 풀도록 하는 알고리즘”
( 이름이 Dynamic Programming 인 이유는 이름은 그냥 멋있어 보여서 그렇게 지었다고 한다. )
Dynamic Programming => DP 의 가장 대표적인 예로는 피보나치 수열을 들 수 있다.
https://ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98 <- 피보나치 수열

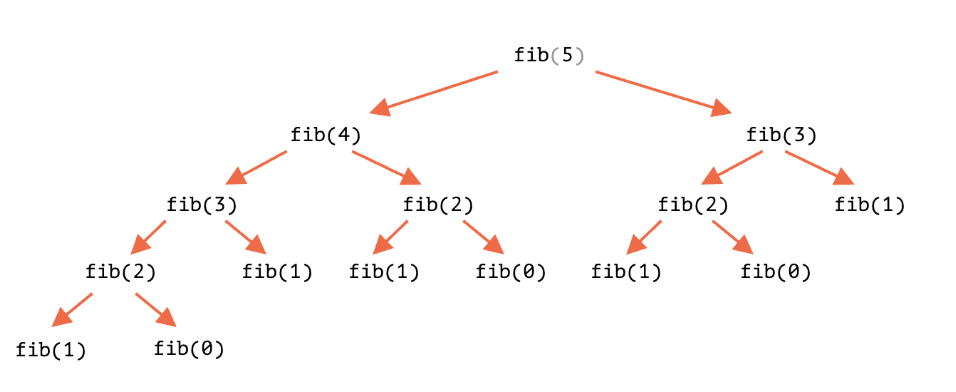
Fibonacci Number(피보나치 수열)은 0과 1로 시작하며, 다음 피보나치 수는 바로 앞의 두 피보나치 수의 합이 되는 수열이다.
피보나치 수열은 점화식으로 표현할 수 있기 때문에 재귀함수로 구현할 수 있다.
아래의 코드는 재귀 함수를 이용한 피보나치 수열을 구하는 코드다.
#include <iostream>
using namespace std;
int N, cntOne;
int FibonacciRecursive(int N) // 재귀 호출 방법
{
if (N == 1 || N == 2) {
cntOne++; // 카운트
return 1;
}
else {
return FibonacciRecursive(N - 1) + FibonacciRecursive(N - 2);
}
}
int main()
{
cin >> N;
cntOne = 0;
cout << "f(" << N << ") : " << FibonacciRecursive(N) << "\n"; // 재귀
cout << "실행 횟수 : " << cntOne << "번";
return 0;
}
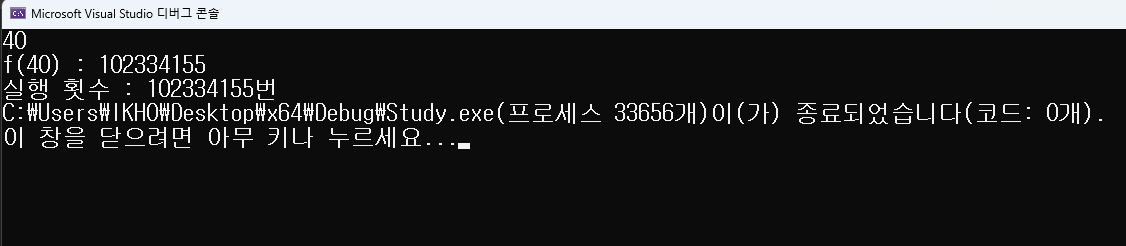
피보나치의 수열의 F(N)에서 N의 값이 증가하면 증가할수록 연산이 기하급수적으로 증가한다.
예를 들어 피보나치의 수열 fib(5) 를 구한다고 하면 아래와 같이 이루어진다.
fib(5)
fib(4) + fib(3)
(fib(3) + fib(2)) + (fib(2) + fib(1))
((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
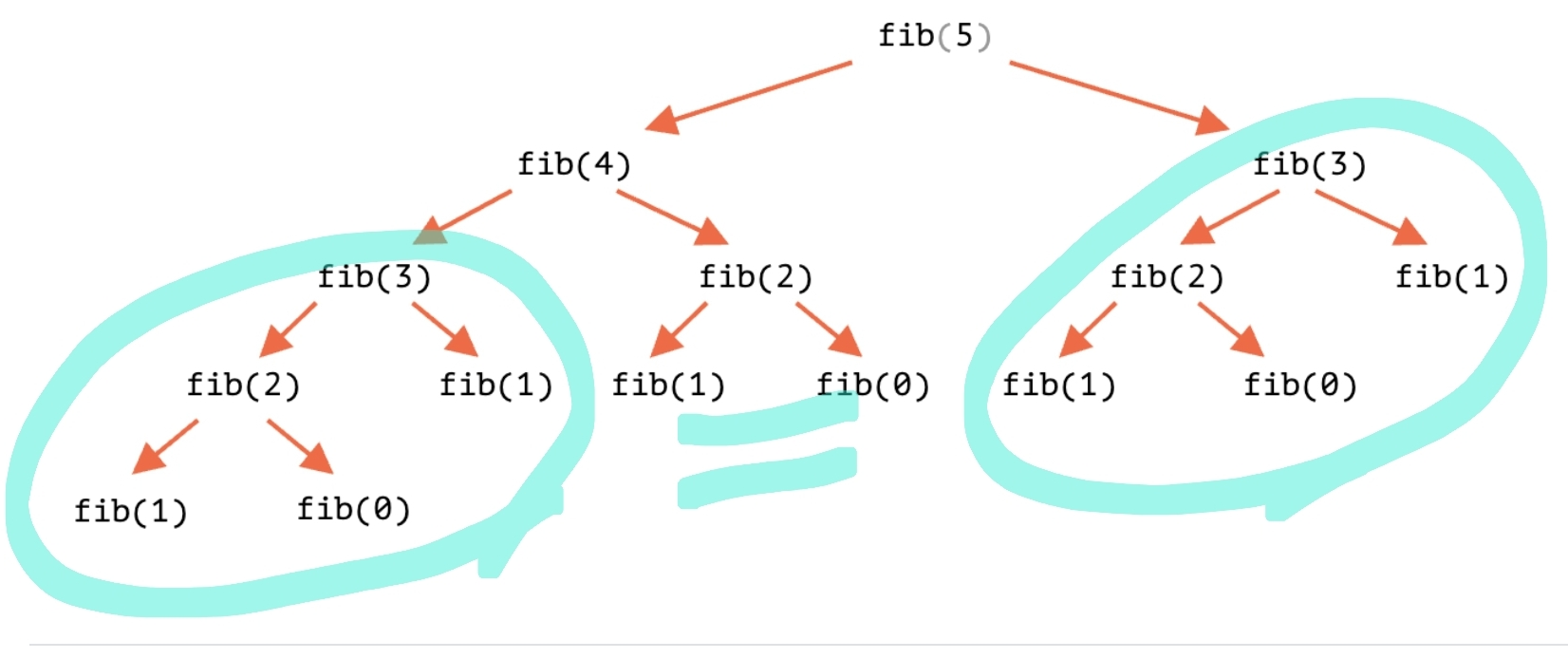
세 번째 줄의 fib(2)가 중복되어 계산되고, 이것은 전체적인 계산 속도를 떨어뜨린다.
결과적으로 이 알고리즘의 시간 복잡도는 지수 함수가 된다.
위와 같은 문제로 DP 알고리즘을 많이 사용하는데
DP는 문제를 여러 개의 하위 문제(subproblem)로 나누고 각 하위 문제의 해결을 계산한 뒤,
그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 중복 계산을 제거하여 효율성을 개선하는 알고리즘이다.
다이내믹 프로그래밍의 대표적인 2가지 방법
https://www.geeksforgeeks.org/tabulation-vs-memoization/
1. Tabulation: Bottom Up (표, 상향식)
2. Memoization: Top Down (메모화, 하향식)
1. Tabulation: Bottom Up (표, 상향식)
이름 자체에서 알 수 있듯이 바닥에서 시작하여 상단으로 답을 축적하여 해결한다.
(가장 작은 문제들부터 차례 차례 답을 쌓아 올려가기 때문에 Bottom Up)
피보나치 수열을 예로 들면
F(0) 부터 F(N)까지 F(1), F(2), F(3)…. F(N) 까지 순서대로 차근차근 값을 구하고 구한 값을 이용하여 중복 계산을 제거한다.
#include <iostream>
using namespace std;
int N, cnt = 0;
int arr[41];
int main()
{
cin >> N;
arr[1] = arr[2] = 1;
for (int i = 3; i <= N; i++) {
cnt++;
arr[i] = arr[i - 1] + arr[i - 2];
}
cout << "F(" << N << ") = " << arr[N] << " // 실행 수 : " << cnt << "번";
return 0;
}

재귀의 102,334,155번 연산 수와 비교하면 엄청난 차이를 보인다.
2. Memoization: Top Down (메모화, 하향식)
Memoization 방식은 목표에서 시작하여 가까운 값을 찾아 탑다운 형태로 중복된 값을 사용한다.
(가장 먼저 호출하는 문제는 가장 큰 문제이기 때문에 Top – Down)
#include <iostream>
using namespace std;
int N, cnt = 0;
int arr[41];
int FibonacciDP(int x)
{
if (x == 0) return 0;
else if (x == 1) return 1;
cnt++; // 연산 카운트
if (arr[x] == 0) return arr[x] = FibonacciDP(x - 1) + FibonacciDP(x - 2);
else return arr[x];
}
int main()
{
cin >> N;
arr[1] = arr[2] = 1;
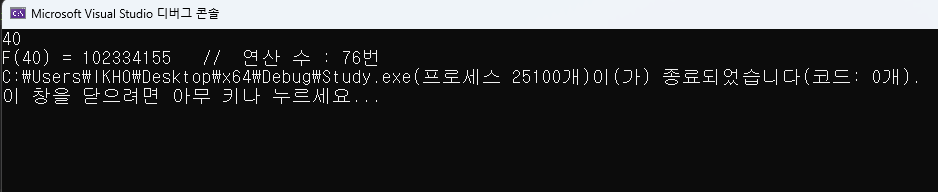
cout << "F(" << N << ") = " << FibonacciDP(N) << " // 연산 수 : " << cnt << "번";
return 0;
}
계산한 적이 있다면 추가 재귀 호출 없이 그 값을 바로 리턴 아니라면 지금 계산해서 그 값을 넣어 준다.
(arr[x] = 0 이라면 계산한 적이 없다는 뜻)
한 번 계산했던 값은 두 번 다시 계산할 필요가 없으므로, f(N)을 구하는 데 O(N)의 복잡도가 필요하다.





핑백: 백준 2193번 (이친수, C++, DP) [BAEKJOON] - 어제와 내일의 나 그 사이의 이야기