알고리즘을 분석하는 이유
정확성 확인(무결성 확인)
모든 유효한 입력에 대해서 유한 시간 내에 올바른 해를 찾아내는가를 판단하기 위함
효율성 확인
한정된 자원(기억 장소 사용량, 수행 시간)에서 효율적으로 작동하는지 확인하기 위함
궁극적으로 알고리즘을 분석하여 얻는 이점
문제를 해결하기 위해 중요한 것과 중요하지 않은 것을 판단할 수 있다.
문제를 단순화하여 생각할 수 있다.
다른 사람의 아이디어에 대한 효율성을 판단할 수 있다.
같은 문제를 해결하는 알고리즘은 여러 가지가 존재한다.
최상의 알고리즘은 존재하지 않으며 항상 주어진 상황을 객관적으로 분석하여 알고리즘을 선택해야 한다.
또한 기존의 알고리즘을 개선하기 위해서 적용 가능한 여러 알고리즘을 객관적으로 비교 분석을 할 줄 알아야 한다.
알고리즘을 분석하는 방법
일반적으로 알고리즘의 수행 시간에 따른 시간복잡도(Time Complexity)와
작성한 프로그램이 얼마나 많은 공간(메모리)을 차지하느냐를 분석하는 방법인 공간복잡도(Space Complexity)로 분석한다.
시간복잡도의 경우 알고리즘을 잘못 구성하였을 경우 결과값이 나오지 않거나 현저하게 느린속도가 나오기에
공간복잡도보다는 시간복잡도를 우선시하여 프로그램을 분석한다. (기술의 발달로 인한 메모리 증가도 큰 영향)
알고리즘의 수행 시간
알고리즘의 효율성을 분석하는 방법은 다양하지만, 많은 경우에 알고리즘의 수행 시간을 이용하여 효율성을 분석
시간복잡도 (Time Complexity) : 얼마나 빠른가?
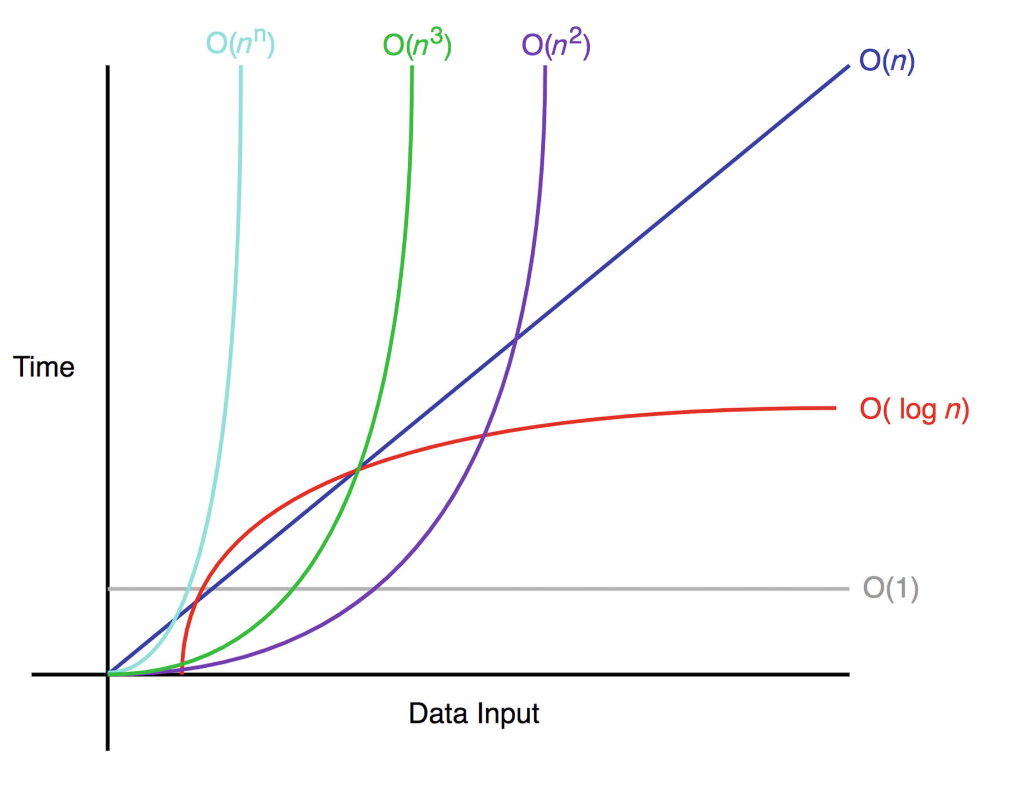
입력 크기에 비례하여 작업시간이 어떠한 비율로 증가하는지 확인한다.
시간복잡도를 사용하는 이유
실측으로 시간을 측정하는 경우 프로그래밍 언어, 컴퓨터의 성능, 프로그래머의 실력 등의 다양한 변수에 따라 달라질 수 있다.
(분석에 객관적인 기준이 필요)
수행 시간 분석 방법
최선 경우 분석(Best Case Analysis) => Big-Ω(빅-오메가) / 하한 점근
최선의 경우는 프로그램 실행 시간의 하한을 계산한다.
선형 탐색의 경우 베스트 케이스는 찾으려는 x가 제일 처음에 위치하는 경우이다.
최상의 경우 실행되는 연산의 수는 상수이며 입력 크기 n에 영향을 받지 않는다.
따라서 최상의 경우 시간 복잡도는 θ(1)이다.
최악 경우 분석(Worst Case Analysis) => Big-O(빅-오) / 상한 점근
최악의 경우는 알고리즘이 실행되는 시간의 상한을 결정한다.
프로그램을 실행 할 때 연산이 수행되는 횟수가 최대가 되는 경우이다.
선형 탐색의 경우 찾으려는 원소가 배열에 존재하지 않거나 배열의 끝에 존재하는 경우이다.
배열에 찾으려는 원소가 존재하지 않으면 배열의 전체 원소와 모두 비교를 한다.
이 때 최악이라는 것은 단위 연산이 수행되는 횟수가 최대라는 것이다.
입력 크기와 입력 값(내용) 모두에 종속된다.
선형 탐색의 최악의 경우 시간 복잡도는 θ(n)이다.
평균 경우 분석(Average Case Analysis) => Big-θ(빅-세타) / 그 둘의 평균
평균적인 경우를 계산하는 방법은 다음과 같다.
가능한 모든 입력에 대해 실행 시간을 계산한다.
그리고 이 시간을 모두 더하고, 더한 결과를 입력의 수로 나눈다.
선형 탐색을 계산하는 방법은 다음과 같다.
선형 탐색인 경우 모든 경우들이 균등하게 분포한다고 가정하자.
크기 n의 배열에서 원소 x를 찾으려고 할 때, x의 위치는 1 또는 2, 3, … , n이 될 수 있다.
배열을 따라 각 원소를 x와 비교한다.
만약 배열의 k번째 원소에 도달 했으면 이미 k번 비교를 한 것이다.
x가 인덱스 1의 위치에 있다면 1번 비교한다.
x가 인덱스 2의 위치에 있다면 2번 비교한다.
…
x가 인덱스 n의 위치에 있다면 n번 비교한다.
평균을 구하기 위해 비교한 수들을 합하면 1+ 2 + 3 + … + n = (n+1)n / 2
이를 배열의 크기인 n으로 나누면 (n+1) / 2 이다.
따라서 선형 탐색의 평균 시간 복잡도는 θ(n) 이다.
가장 자주 사용되는 분석
최악 경우 분석(Worst Case Analysis) => Big-O(빅-오) / 상한 점근
시간 복잡도에는 여러 개념이 있지만 그중에서
‘아무리 많이 걸려도 이 시간 안에는 끝날 것‘의 개념이 제일 중요하다.
예를 들어 동전을 튕겨서 뒷면이 나올 확률을 이야기해본다면 운이 좋으면 한 번에 뒷면이 나올 수도 있고
운이 좋지 않으면 3번 4번만에 뒷면이 나올수도 있다.
운이 나쁜 경우 n번만큼 동전을 튕겨야 하는 최악의 경우가 발생하는데
이 최악의 경우를 계산하는 방식을 빅-오(Big-O) 표기법이라고 부르며 이 방식을 가장 많이 사용한다.



