가장 긴 증가하는 부분 수열 5 
https://www.acmicpc.net/problem/14003
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 3 초 | 512 MB | 45574 | 15974 | 11322 | 34.533% |
문제
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다.
둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)
출력
첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.
둘째 줄에는 정답이 될 수 있는 가장 긴 증가하는 부분 수열을 출력한다.
예제 입력 1
6 10 20 10 30 20 50
예제 출력 1
4 10 20 30 50
출처
- 문제를 만든 사람: baekjoon
- 데이터를 추가한 사람: harinboy, jh05013, kkw564, ldw0318, minho6428, sohnryang, surung9898, yeo2507
- 빠진 조건을 찾은 사람: Acka
비슷한 문제
- 11053번. 가장 긴 증가하는 부분 수열
- 11054번. 가장 긴 바이토닉 부분 수열
- 11055번. 가장 큰 증가하는 부분 수열
- 11722번. 가장 긴 감소하는 부분 수열
- 12015번. 가장 긴 증가하는 부분 수열 2
- 12738번. 가장 긴 증가하는 부분 수열 3
- 14002번. 가장 긴 증가하는 부분 수열 4
알고리즘 분류
1차 시도 – 로직 그대로 구현

한 번의 입력(num)에 의해 생성된 새로운 시퀀스들을 임시로 저장
어떤 수열에도 붙을 수 없으면 독립된 시퀀스 시작
나중에 불필요한 시퀀스(같은 길이인데 꼬리가 큰 것)는 제거
#include <iostream>
#include <vector>
using namespace std;
int n; // 수열의 개수
vector<vector<int>> Sequences;
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
if (n <= 0) return 0;
int num;
cin >> num;
// 첫 번째 수로 초기 시퀀스 하나 생성
vector<int> sequence;
sequence.push_back(num);
Sequences.push_back(sequence);
for (int i = 1; i < n; i++)
{
cin >> num;
int length = Sequences.size();
bool canExtend = false;
vector<vector<int>> newSequences;
// 기존 시퀀스들을 모두 검사
for (int j = 0; j < length; j++)
{
int last = Sequences[j].back();
// 확장 가능한 경우 : 새로운 시퀀스 생성
if (last < num)
{
canExtend = true;
vector<int> extendedSeq = Sequences[j];
extendedSeq.push_back(num);
newSequences.push_back(extendedSeq);
}
}
// 어떤 시퀀스에도 붙지 못하면 새로운 시퀀스 시작
if (!canExtend)
{
vector<int> newSeq;
newSeq.push_back(num);
newSequences.push_back(newSeq);
}
// 새로 생긴 시퀀스들을 기존에 합침
for (auto& seq : newSequences)
Sequences.push_back(seq);
// 최적 시퀀스 길이 및 꼬리값 계산
int maxSeqSize = 0;
int bestIndex = 0;
int bestTail = 1000000001;
for (int j = 0; j < (int)Sequences.size(); j++)
{
int sz = Sequences[j].size();
int tail = Sequences[j].back();
if (sz > maxSeqSize || (sz == maxSeqSize && tail < bestTail))
{
maxSeqSize = sz;
bestTail = tail;
bestIndex = j;
}
}
// 가지치기: 같은 길이인데 꼬리값이 큰 시퀀스 제거
for (int j = 0; j < (int)Sequences.size();)
{
int sz = Sequences[j].size();
int tail = Sequences[j].back();
if (sz == maxSeqSize && tail > bestTail)
{
Sequences.erase(Sequences.begin() + j);
}
else
{
j++;
}
}
}
// 결과 중 가장 긴 시퀀스 찾기
int maxSize = 0;
int bestIdx = 0;
for (int i = 0; i < (int)Sequences.size(); i++)
{
if (Sequences[i].size() > maxSize)
{
maxSize = Sequences[i].size();
bestIdx = i;
}
}
cout << maxSize << "\n";
for (int x : Sequences[bestIdx])
cout << x << " ";
return 0;
}
브루트포스 방식으로 모든 가능한 증가 수열을 시도하는 방법은 시간 초과 및 메모리 초과로 인하여 통과할 수 없음.
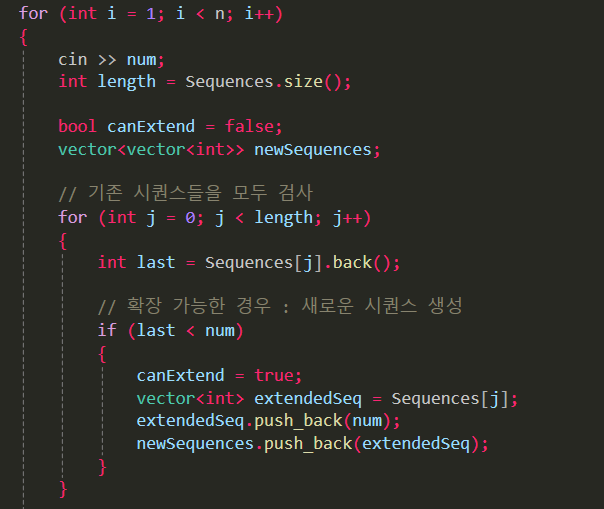
매 반복마다 Sequences의 크기가 기하급수적으로 늘어나는 구조
n개의 원소가 들어오면 2ⁿ에 비례하는 시퀀스로 통과하기 힘들다. (O(2ⁿ))
| 단계 | 가능한 Sequences 수 |
|---|---|
| 1 | [ [1] ] |
| 2 | [ [1], [2], [1,2] ] |
| 3 | [ [1], [2], [3], [1,2], [1,3], [2,3], [1,2,3] ] |
| 4 | 거의 모든 가능한 증가 부분 수열이 등장함 (약 15개) |
2차 시도 – 이분 탐색 + 인덱스 추적을 이용한 LIS 복원 / O(N log N)

최장 증가 수열 (LIS, Longest Increasing Subsequence)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// (LIS, Longest Increasing Subsequence)
int main()
{
ios::sync_with_stdio(false);
std::cin.tie(NULL);
std::cout.tie(NULL);
int N;
std::cin >> N;
vector<int> input(N);
for (int i = 0; i < N; i++)
std::cin >> input[i];
vector<int> tail; // LIS를 구성하는 인덱스들
vector<int> prev_idx(N, -1); //각 요소가 LIS에 포함될 때, 그 직전 요소의 인덱스를 저장
for (int i = 0; i < N; i++)
{
// 이분 탐색으로 input[i]가 tail 배열에서 들어가야 할 위치 찾기
int lo = 0;
int hi = (int)tail.size() - 1;
int pos = (int)tail.size(); // 기본값은 맨 뒤
while (lo <= hi)
{
int mid = (lo + hi) / 2;
// input[i]보다 크거나 같은 첫 번째 tail 원소 위치(pos)를 찾
if (input[tail[mid]] < input[i])
{
lo = mid + 1;
}
else
{
pos = mid;
hi = mid - 1;
}
}
// 이전 인덱스 설정
if (pos > 0)
{
prev_idx[i] = tail[pos - 1];
}
else
{
prev_idx[i] = -1; // 첫 번째 요소
}
// tail 업데이트
if (pos == (int)tail.size())
{
tail.push_back(i);
}
else
{
tail[pos] = i;
}
}
// 결과: LIS 길이
int lis_len = (int)tail.size();
std::cout << lis_len << "\n";
// 실제 LIS 수열 재구성
vector<int> lis;
for (int idx = tail.back(); idx != -1; idx = prev_idx[idx])
{
lis.push_back(input[idx]);
}
reverse(lis.begin(), lis.end());
for (int v : lis)
std::cout << v << " ";
std::cout << "\n";
return 0;
}
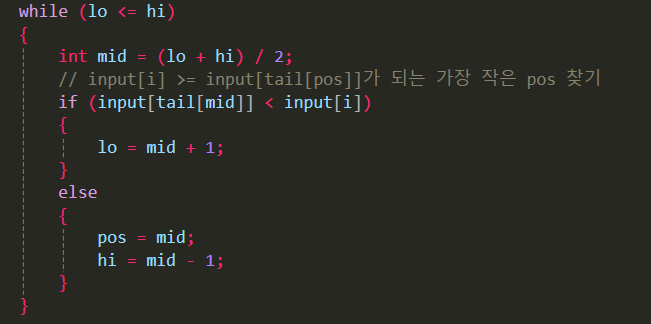
input[i]가 들어가야 할 위치(pos)를 찾음
즉, tail 배열 내에서 input[i]보다 작지만 가장 큰 값 다음 위치를 찾는다.
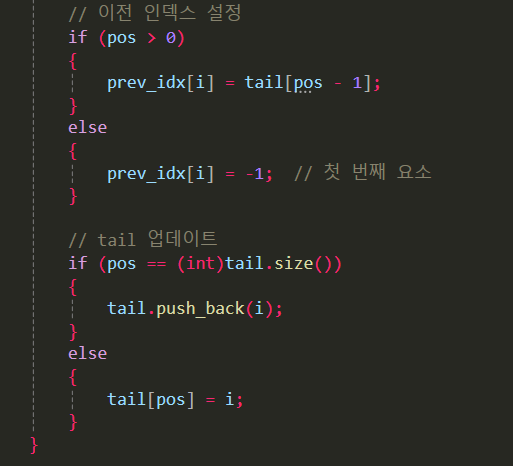
prev_idx[i]는 input[i] 바로 앞에 올 LIS 원소의 인덱스입니다.
pos > 0이면 → 현재 원소가 “길이 pos+1″짜리 LIS의 마지막이 되므로 “그 바로 이전 원소”는 tail[pos - 1]
pos == 0이면 → 수열의 첫 번째 원소이므로 이전이 없음
pos == tail.size() → input[i]가 지금 까지의 모든 수보다 크므로 LIS 길이 1 증가
그렇지 않으면 → 기존 LIS 후보 중 “끝값이 더 큰 것”을 input[i]로 치환 (더 작은 끝값 유지)
예시 1
input = [5, 2, 8, 6, 3, 6, 9, 7]
| 단계 | i | input[i] | tail (인덱스) | tail (값으로 표현) | prev_idx | 설명 |
|---|---|---|---|---|---|---|
| 0 | 0 | 5 | [0] | [5] | [-1, ?, ?, ?, ?, ?, ?, ?] | 첫 번째 원소 → 새로운 LIS 시작 |
| 1 | 1 | 2 | [1] | [2] | [-1, -1, ?, ?, ?, ?, ?, ?] | 2 < 5 → 기존 tail[0] 교체 (더 작은 끝값 유지) |
| 2 | 2 | 8 | [1, 2] | [2, 8] | [-1, -1, 1, ?, ?, ?, ?, ?] | 8 > 2 → 길이 2짜리 LIS 형성 |
| 3 | 3 | 6 | [1, 3] | [2, 6] | [-1, -1, 1, 1, ?, ?, ?, ?] | 6은 2보다 크지만 8보다 작음 → 8을 6으로 교체 |
| 4 | 4 | 3 | [1, 4] | [2, 3] | [-1, -1, 1, 1, 1, ?, ?, ?] | 3은 2보다 크고 6보다 작음 → 6을 3으로 교체 |
| 5 | 5 | 6 | [1, 4, 5] | [2, 3, 6] | [-1, -1, 1, 1, 1, 4, ?, ?] | 6은 3보다 크므로 길이 3짜리 LIS 생성 |
| 6 | 6 | 9 | [1, 4, 5, 6] | [2, 3, 6, 9] | [-1, -1, 1, 1, 1, 4, 5, ?] | 9 > 6 → 길이 4짜리 LIS 생성 |
| 7 | 7 | 7 | [1, 4, 5, 7] | [2, 3, 6, 7] | [-1, -1, 1, 1, 1, 4, 5, 5] | 7은 6보다 크지만 9보다 작음 → 9를 7로 교체 |
예시 2
이분 탐색을 이용한 LIS 구성 로직 input = [3, 5, 2, 7, 4, 1, 8] -------------------------------- i=0 (값: 3) tail: [] (빈 배열) 이분탐색: tail.size() = 0 → while문 스킵 pos = 0 (기본값) prev_idx[0] = -1 (pos=0이므로) tail 업데이트: pos == tail.size() → push_back(0) 결과: tail = [0] (값: [3]) -------------------------------- i=1 (값: 5) tail: [0] (값: [3]) 이분탐색: lo=0, hi=0, mid=0 input[tail[0]] = 3 < 5 → lo = mid+1 = 1 lo=1 > hi=0 → 종료 pos = tail.size() = 1 prev_idx[1] = tail[0] = 0 (5 앞에 3) tail 업데이트: push_back(1) 결과: tail = [0,1] (값: [3,5]) -------------------------------- i=2 (값: 2) tail: [0,1] (값: [3,5]) 이분탐색: lo=0, hi=1, mid=0 input[tail[0]] = 3 >= 2 → pos=0, hi=-1 lo=0 > hi=-1 → 종료 pos = 0 prev_idx[2] = -1 (pos=0이므로) tail 업데이트: tail[0] = 2 결과: tail = [2,1] (값: [2,5]) -------------------------------- i=3 (값: 7) tail: [2,1] (값: [2,5]) 이분탐색: lo=0, hi=1, mid=0: input[tail[0]]=2 < 7 → lo=1 lo=1, hi=1, mid=1: input[tail[1]]=5 < 7 → lo=2 lo=2 > hi=1 → 종료 pos = tail.size() = 2 prev_idx[3] = tail[1] = 1 (7 앞에 5) tail 업데이트: push_back(3) 결과: tail = [2,1,3] (값: [2,5,7]) -------------------------------- i=4 (값: 4) tail: [2,1,3] (값: [2,5,7]) 이분탐색: lo=0, hi=2, mid=1: input[tail[1]]=5 >= 4 → pos=1, hi=0 lo=0, hi=0, mid=0: input[tail[0]]=2 < 4 → lo=1 lo=1 > hi=0 → 종료 pos = 1 prev_idx[4] = tail[0] = 2 (4 앞에 2) tail 업데이트: tail[1] = 4 결과: tail = [2,4,3] (값: [2,4,7]) -------------------------------- i=5 (값: 1) tail: [2,4,3] (값: [2,4,7]) 이분탐색: lo=0, hi=2, mid=1: input[tail[1]]=4 >= 1 → pos=1, hi=0 lo=0, hi=0, mid=0: input[tail[0]]=2 >= 1 → pos=0, hi=-1 lo=0 > hi=-1 → 종료 pos = 0 prev_idx[5] = -1 tail 업데이트: tail[0] = 5 결과: tail = [5,4,3] (값: [1,4,7]) -------------------------------- i=6 (값: 8) tail: [5,4,3] (값: [1,4,7]) 이분탐색: lo=0, hi=2, mid=1: input[tail[1]]=4 < 8 → lo=2 lo=2, hi=2, mid=2: input[tail[2]]=7 < 8 → lo=3 lo=3 > hi=2 → 종료 pos = tail.size() = 3 prev_idx[6] = tail[2] = 3 (8 앞에 7) tail 업데이트: push_back(6) 결과: tail = [5,4,3,6] (값: [1,4,7,8])

![백준 26068번 (치킨댄스를 추는 곰곰이를 본 임스 2, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og-1.png)
![Programmers 17685 [3차] 자동완성 [2018 KAKAO BLIND RECRUITMENT]](https://lycos7560.com/wp-content/uploads/2023/03/programmers.jpg)
이 글은 LIS 알고리즘의 꿈과 현실을 정확히 보여줍니다. 브루트포스는 시간 초과로 절망적이지만, 이분 탐색은 놀라운 성능을 자랑한다. 코드 예시만 보면 이분 탐색이 마술 같다고 감탄하지 않을 수 없네요. 특히 `tail` 배열 업데이트 부분이 마치 수열 왕국의 시장에서 최선의 가격을 찾는 것 같아서 웃겼습니다. 물론 실제 코딩 테스트에서는 이분 탐색의 씨름을 무릅쓰고 `prev_idx` 배열을 잘못 다루는 실수가 허락되지 않겠죠. 그래도 이 글이 LIS의 위대함을 아주 잘 보여준다니, 정말 알고리즘의 로망입니다!đồng hồ online