양과 늑대
https://school.programmers.co.kr/learn/courses/30/lessons/92343
문제 설명
2진 트리 모양 초원의 각 노드에 늑대와 양이 한 마리씩 놓여 있습니다.
이 초원의 루트 노드에서 출발하여 각 노드를 돌아다니며 양을 모으려 합니다.
각 노드를 방문할 때 마다 해당 노드에 있던 양과 늑대가 당신을 따라오게 됩니다.
이때, 늑대는 양을 잡아먹을 기회를 노리고 있으며,
당신이 모은 양의 수보다 늑대의 수가 같거나 더 많아지면 바로 모든 양을 잡아먹어 버립니다.
당신은 중간에 양이 늑대에게 잡아먹히지 않도록 하면서 최대한 많은 수의 양을 모아서 다시 루트 노드로 돌아오려 합니다.
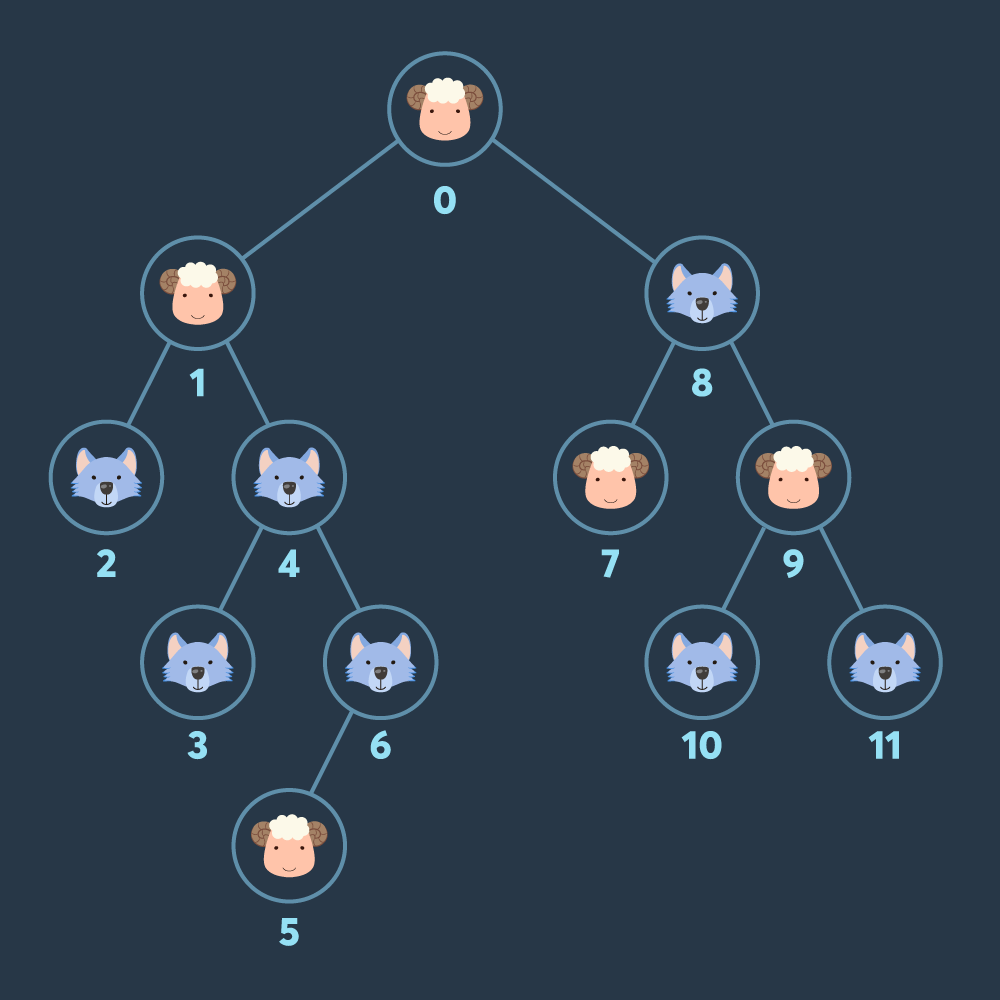
예를 들어, 위 그림의 경우(루트 노드에는 항상 양이 있습니다) 0번 노드(루트 노드)에서 출발하면 양을 한마리 모을 수 있습니다.
다음으로 1번 노드로 이동하면 당신이 모은 양은 두 마리가 됩니다. 이때, 바로 4번 노드로 이동하면 늑대 한 마리가 당신을 따라오게 됩니다.
아직은 양 2마리, 늑대 1마리로 양이 잡아먹히지 않지만, 이후에 갈 수 있는 아직 방문하지 않은 모든 노드(2, 3, 6, 8번)에는 늑대가 있습니다.
이어서 늑대가 있는 노드로 이동한다면(예를 들어 바로 6번 노드로 이동한다면) 양 2마리, 늑대 2마리가 되어 양이 모두 잡아먹힙니다.
여기서는 0번, 1번 노드를 방문하여 양을 2마리 모은 후, 8번 노드로 이동한 후(양 2마리 늑대 1마리) 이어서 7번, 9번 노드를 방문하면 양 4마리 늑대 1마리가 됩니다.
이제 4번, 6번 노드로 이동하면 양 4마리, 늑대 3마리가 되며, 이제 5번 노드로 이동할 수 있게 됩니다. 따라서 양을 최대 5마리 모을 수 있습니다.
각 노드에 있는 양 또는 늑대에 대한 정보가 담긴 배열 info, 2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열 edges가 매개변수로 주어질 때,
문제에 제시된 조건에 따라 각 노드를 방문하면서 모을 수 있는 양은 최대 몇 마리인지 return 하도록 solution 함수를 완성해주세요.
제한사항
- 2 ≤
info의 길이 ≤ 17info의 원소는 0 또는 1 입니다.- info[i]는 i번 노드에 있는 양 또는 늑대를 나타냅니다.
- 0은 양, 1은 늑대를 의미합니다.
- info[0]의 값은 항상 0입니다. 즉, 0번 노드(루트 노드)에는 항상 양이 있습니다.
edges의 세로(행) 길이 =info의 길이 – 1edges의 가로(열) 길이 = 2edges의 각 행은 [부모 노드 번호, 자식 노드 번호] 형태로, 서로 연결된 두 노드를 나타냅니다.- 동일한 간선에 대한 정보가 중복해서 주어지지 않습니다.
- 항상 하나의 이진 트리 형태로 입력이 주어지며, 잘못된 데이터가 주어지는 경우는 없습니다.
- 0번 노드는 항상 루트 노드입니다.
입출력 예
| info | edges | result |
|---|---|---|
| [0,0,1,1,1,0,1,0,1,0,1,1] | [[0,1],[1,2],[1,4],[0,8],[8,7],[9,10],[9,11],[4,3],[6,5],[4,6],[8,9]] | 5 |
| [0,1,0,1,1,0,1,0,0,1,0] | [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6],[3,7],[4,8],[6,9],[9,10]] | 5 |
입출력 예 설명
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
주어진 입력은 다음 그림과 같습니다.

0번 – 2번 – 5번 – 1번 – 4번 – 8번 – 3번 – 7번 노드 순으로 이동하면 양 5마리 늑대 3마리가 됩니다.
여기서 6번, 9번 노드로 이동하면 양 5마리, 늑대 5마리가 되어 양이 모두 잡아먹히게 됩니다.
따라서 늑대에게 잡아먹히지 않도록 하면서 최대로 모을 수 있는 양은 5마리입니다.
제한시간 안내
- 정확성 테스트 : 10초
통과된 코드
Set에 현재 상황에서 갈 수 있는 노드를 전부 저장하여 완전 탐색을 수행
#include <string>
#include <vector>
#include <iostream>
#include <set>
using namespace std;
struct MyNode;
vector<MyNode> _AllNodeV;
int answer = 0;
struct MyNode
{
// 노드의 번호, 동물의 타입
int _Num, _Type;
vector<MyNode*> _ChildnodeV; // 자식 노드
MyNode(int _num, int _type) {
_Num = _num;
_Type = _type;
}
};
// set에 갈 수 있는 노드의 번호를 넣어주면서 DFS 탐색을 통하여 완전 탐색
void CustomDFS(int _cnt, int _sheep, int _wolf, set<int> _nodeSet) {
if (_AllNodeV[_cnt]._Type) _wolf++;
else _sheep++; // 늑대는 1, 양은 0
if (_wolf >= _sheep) return; // 늑대가 같거나 크다면 return
if (_sheep > answer) answer = _sheep; // 최댓값 갱신
_nodeSet.erase(_cnt); // 방문한 곳을 지워준다.
for (auto& it : _AllNodeV[_cnt]._ChildnodeV)
_nodeSet.insert(it->_Num); // 다음 갈 곳을 추가
for (auto& it : _nodeSet)
CustomDFS(it, _sheep, _wolf, _nodeSet);
}
int solution(vector<int> info, vector<vector<int>> edges) {
for (int i = 0; i < info.size(); i++) { // 노드 생성
MyNode _node = MyNode(i, info[i]);
_AllNodeV.push_back(_node);
}
for (int i = 0; i < edges.size(); i++) // 자식 노드 입력
_AllNodeV[edges[i][0]]._ChildnodeV.push_back(&_AllNodeV[edges[i][1]]);
set<int> _StartSet;
_StartSet.insert(0); // 0번 노드부터 시작
CustomDFS(0, 0, 0, _StartSet);
return answer;
}


![백준 2525번 (오븐 시계, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og-1.png)
![백준 2225번 (합분해, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)
![백준 10809번 (알파벳 찾기, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/2022/10/boj-og-1-2048x1070-1-1024x535.png)