지름길

https://www.acmicpc.net/problem/1446

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
2 초	128 MB	5137	2633	1998	50.995%

문제

매일 아침, 세준이는 학교에 가기 위해서 차를 타고 D킬로미터 길이의 고속도로를 지난다.

이 고속도로는 심각하게 커브가 많아서 정말 운전하기도 힘들다.

어느 날, 세준이는 이 고속도로에 지름길이 존재한다는 것을 알게 되었다.

모든 지름길은 일방통행이고, 고속도로를 역주행할 수는 없다.

세준이가 운전해야 하는 거리의 최솟값을 출력하시오.

입력

첫째 줄에 지름길의 개수 N과 고속도로의 길이 D가 주어진다.

N은 12 이하인 양의 정수이고, D는 10,000보다 작거나 같은 자연수이다.

다음 N개의 줄에 지름길의 시작 위치, 도착 위치, 지름길의 길이가 주어진다.

모든 위치와 길이는 10,000보다 작거나 같은 음이 아닌 정수이다.

지름길의 시작 위치는 도착 위치보다 작다.

출력

세준이가 운전해야하는 거리의 최솟값을 출력하시오.

예제 입력 1

5 150
0 50 10
0 50 20
50 100 10
100 151 10
110 140 90

예제 출력 1

70

예제 입력 2

2 100
10 60 40
50 90 20

예제 출력 2

80

예제 입력 3

8 900
0 10 9
20 60 45
80 190 100
50 70 15
160 180 14
140 160 14
420 901 5
450 900 0

예제 출력 3

432

출처

• 문제를 번역한 사람: baekjoon
• 문제를 다시 작성한 사람: jh05013

알고리즘 분류

• 다이나믹 프로그래밍
• 그래프 이론
• 데이크스트라

---

기본적인 로직은 Dujkstra 알고리즘을 기반으로 한다.

알고리즘 – 다익스트라/데이크스트라(Dijkstra) 알고리즘 정리 (길찾기)

---

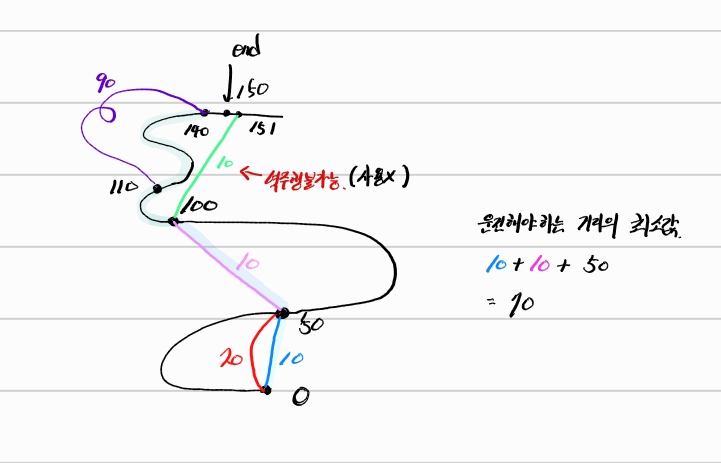
주의사항

주의할 점은 역주행이 불가능하다는 점 (현재 위치에서 지름길을 더한 값이 목적지를 넘어가면 안된다.)

또 지름길이 순서대로 이쁘게 주어지지 않는다. (정렬을 해서 처리하는 것도 하나의 방법)

내 풀이는 최단경로 테이블을 갱신하면 목적지 그 이후의 값을 dist[]가 더 적거나 목적지까지 +1 해주면서 업데이트 해주었다.

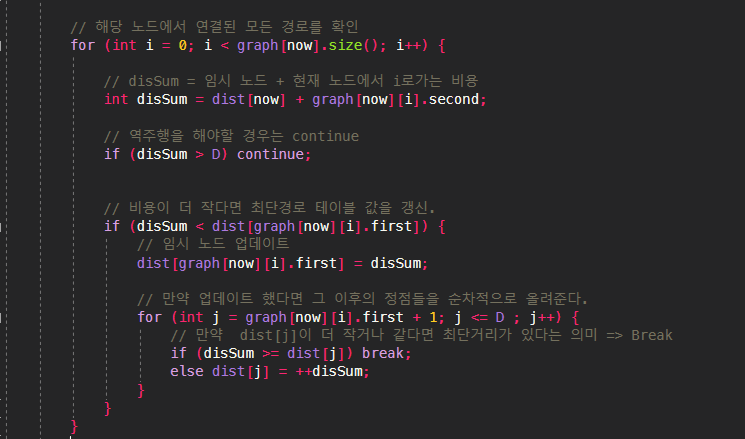
통과된 코드

#include <iostream>
#include <vector>

using namespace std;

constexpr int MAXN = 10001;

// 지름길의 개수 N, 고속도로의 길이 D
int N, D;

int A, B, C;

/*
각 노드에 연결되어 있는 노드에 대한 정보를 담는 벡터
a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].push_back({b, c});
*/
vector<pair<int, int>> graph[MAXN];

// 임시 노드
int dist[MAXN];

int main()
{
	// cin.tie(null); 코드는 cin과 cout의 묶음을 풀어줍니다.
	// scanf와 동기화를 비활성화
	ios_base::sync_with_stdio(false); 
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> N >> D;

	for (int i = 0; i < N; i++) {
		cin >> A >> B >> C;
		graph[A].push_back(make_pair(B, C));
	}

	// 기본 초기화
	for (int i = 0; i < MAXN; i++) dist[i] = i;

	int now = 0;
	while (true) {

		if (now == D) { 
			// 목적지에 도착했으므로 결과를 출력
			cout << dist[now];
			break;
		}

		// 해당 노드에서 연결된 모든 경로를 확인
        for (int i = 0; i < graph[now].size(); i++) {

            // disSum = 임시 노드 + 현재 노드에서 i로가는 비용
            int disSum = dist[now] + graph[now][i].second;
			
			// 역주행을 해야할 경우는 continue
			if (disSum > D) continue; 


            // 비용이 더 작다면 최단경로 테이블 값을 갱신.
            if (disSum < dist[graph[now][i].first]) {
                // 임시 노드 업데이트
				dist[graph[now][i].first] = disSum;

				// 만약 업데이트 했다면 그 이후의 정점들을 순차적으로 올려준다.
				for (int j = graph[now][i].first + 1; j <= D ; j++) {
					// 만약  dist[j]이 더 작거나 같다면 최단거리가 있다는 의미 => Break
					if (disSum >= dist[j]) break;
					else dist[j] = ++disSum;
				}
            }
        }

		now++;
	}

	return 0;
}

dijkstra 알고리즘이 익숙하지 않아 해결하는데 오래 걸렸다…