가운데를 말해요 
https://www.acmicpc.net/problem/1655
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 0.1 초 | 128 MB | 80245 | 24515 | 18393 | 31.195% |
문제
백준이는 동생에게 “가운데를 말해요” 게임을 가르쳐주고 있다.
백준이가 정수를 하나씩 외칠때마다 동생은 지금까지 백준이가 말한 수 중에서 중간값을 말해야 한다.
만약, 그동안 백준이가 외친 수의 개수가 짝수개라면 중간에 있는 두 수 중에서 작은 수를 말해야 한다.
예를 들어 백준이가 동생에게 1, 5, 2, 10, -99, 7, 5를 순서대로 외쳤다고 하면, 동생은 1, 1, 2, 2, 2, 2, 5를 차례대로 말해야 한다.
백준이가 외치는 수가 주어졌을 때, 동생이 말해야 하는 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 백준이가 외치는 정수의 개수 N이 주어진다.
N은 1보다 크거나 같고, 100,000보다 작거나 같은 자연수이다.
그 다음 N줄에 걸쳐서 백준이가 외치는 정수가 차례대로 주어진다.
정수는 -10,000보다 크거나 같고, 10,000보다 작거나 같다.
출력
한 줄에 하나씩 N줄에 걸쳐 백준이의 동생이 말해야 하는 수를 순서대로 출력한다.
예제 입력 1
7 1 5 2 10 -99 7 5
예제 출력 1
1 1 2 2 2 2 5
출처
알고리즘 분류
1차 시도 – 배열 인덱스 (실패 / 시간 초과)

배열을 기반으로, 중간값의 인덱스(currentMedian)를 유지하면서 새로운 값이 들어올 때마다 leftCount, rightCount를 조정하는 방식
#include <iostream>
using namespace std;
int n = 0;
int num[20001] = { 0 }; // 값의 출현 횟수 (index = value + 10000)
int currentMedian = 0; // 현재 중간값의 인덱스
int leftCount = 0; // 중간값보다 작은 값들의 개수
int rightCount = 0; // 중간값보다 큰 값들의 개수
// 실제 값 => 배열 인덱스로 변환
inline int GetIndex(int value)
{
return value + 10000;
}
// 배열 인덱스 => 실제 값으로 변환
inline int GetValue(int index)
{
return index - 10000;
}
int FindMedianOptimized(int newValue, int total)
{
int newIdx = GetIndex(newValue);
num[newIdx]++;
// 새 값의 위치에 따라 좌우 카운트 조정
if (newIdx < currentMedian) leftCount++;
else if (newIdx > currentMedian) rightCount++;
else rightCount++; // 같은 값일 경우 간단히 오른쪽으로 분류
// 목표 중간 위치 계산
int targetPos = (total + 1) / 2;
// 중간값 인덱스를 왼쪽으로 이동 (왼쪽 원소가 너무 많을 때)
while (leftCount >= targetPos) {
currentMedian--;
leftCount -= num[currentMedian];
rightCount += num[currentMedian];
}
// 중간값 인덱스를 오른쪽으로 이동 (왼쪽 원소가 부족할 때)
while (leftCount + num[currentMedian] < targetPos) {
leftCount += num[currentMedian];
currentMedian++;
rightCount -= num[currentMedian];
}
// 현재 중간값 반환
return GetValue(currentMedian);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n;
int value = 0;
// 첫 번째 입력값으로 초기화
cin >> value;
num[GetIndex(value)]++;
currentMedian = GetIndex(value);
leftCount = 0;
rightCount = 0;
// 첫 번째 값 => 중간값
cout << value << "\n";
for (int i = 2; i <= n; ++i)
{
cin >> value;
cout << FindMedianOptimized(value, i) << "\n";
}
return 0;
}
시간 초과의 원인
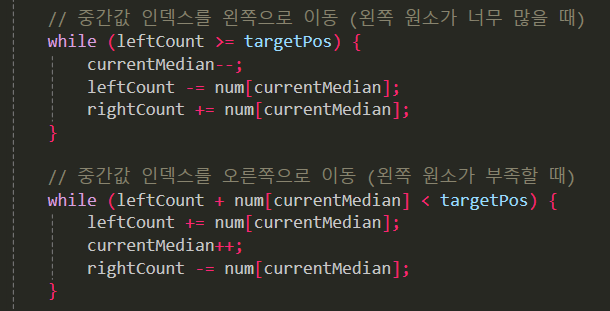
새로운 값이 입력될 때마다 currentMedian을 1씩 이동하며 왼쪽/오른쪽 카운트를 갱신
currentMedian의 이동 거리는 입력된 값의 분포에 따라서 문제가 생길 수 있음.
// 최악의 경우 -10000, -9999, -9998, ... , 9999, 10000
매번 새로운 값이 들어올 때마다 currentMedian이 오른쪽 끝으로 한 칸씩 이동
매번 while 루프가 최대 20,000번 반복되는 불상사가 생길 수 있음
입력 n = 100,000일 때 최악의 복잡도: O(n * 20000) = 2,000,000,000 (20억)
currentMedian 부분을 개선 또는 다른 알고리즘을 사용하는 방법이 더 좋아보임
2차 시도 – Two Heaps 방식 (성공)

maxHeap(왼쪽) + minHeap(오른쪽)으로 균형 유지
maxHeap: 중간값 이하의 값들 저장 (왼쪽 절반)
minHeap: 중간값 이상의 값들 저장 (오른쪽 절반)
균형 조정 시 힙에서 한 번씩 push/pop → O(log n)
#include <iostream>
#include <queue>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
priority_queue<int> maxHeap; // 왼쪽 절반 (최대 힙)
priority_queue<int, vector<int>, greater<int>> minHeap; // 오른쪽 절반 (최소 힙)
for (int i = 0; i < n; ++i)
{
int value;
cin >> value;
// 값 삽입: 왼쪽/오른쪽 균형 유지
if (maxHeap.empty() || value <= maxHeap.top())
maxHeap.push(value);
else
minHeap.push(value);
// 두 힙의 크기 균형 조정 (왼쪽 = 오른쪽 또는 +1)
if (maxHeap.size() > minHeap.size() + 1) {
minHeap.push(maxHeap.top());
maxHeap.pop();
}
else if (minHeap.size() > maxHeap.size()) {
maxHeap.push(minHeap.top());
minHeap.pop();
}
// 현재 중간값 출력
cout << maxHeap.top() << "\n";
}
return 0;
}
입력: [1, 5, 2, 10, -5, 8, 3] 단계별 힙 상태: 1. value=1 maxHeap: [1] minHeap: [] 중간값: 1 2. value=5 maxHeap: [1] minHeap: [5] 중간값: 1 3. value=2 maxHeap: [2, 1] minHeap: [5] 중간값: 2 4. value=10 maxHeap: [2, 1] minHeap: [5, 10] 중간값: 2 5. value=-5 maxHeap: [2, 1, -5] minHeap: [5, 10] 중간값: 2 6. value=8 maxHeap: [2, 1, -5] minHeap: [5, 8, 10] 중간값: 2 7. value=3 maxHeap: [3, 2, -5, 1] minHeap: [5, 8, 10] 중간값: 3

![Programmers 72410 신규 아이디 추천 [2021 KAKAO BLIND RECRUITMENT]](https://lycos7560.com/wp-content/uploads/2023/03/programmers.jpg)
![백준 1991번 (트리 순회, C++) [BAEKJOON]](https://lycos7560.com/wp-content/uploads/boj-og.png)